Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)

Thi Online Đề kiểm tra giữa kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra giữa kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề số 8

4998 lượt thi
5 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Giải các phương trình sau:

a) 3x + 1 = $\frac{- 7}{2}$ .

b) $\frac{x + 4}{5}$ + $\frac{3 x + 2}{10}$ = 7.

c) (3x − 5)² − 2(9x² − 25) = 0.
d) $\frac{x + 1}{x - 2}$ − $\frac{5}{x + 2}$ = $\frac{- 12}{x^{2} - 4}$ + 1.

Xem đáp án

a) 3x + 1 = − $\frac{7}{2}$

$\Leftrightarrow$ 3x = − $\frac{9}{2}$

$\Leftrightarrow$ x = − $\frac{3}{2}$

Vậy tập nghiệm của phương trình là

S = \{- \frac{3}{2}\}

b) $\frac{x + 4}{5}$ + $\frac{3 x + 2}{10}$ = 7 (1)

Û $\frac{2. (x + 4)}{10} + \frac{3 x + 2}{10} = \frac{70}{10}$

Û 2(x + 4) + 3x + 2 = 70

Û 2x + 8 + 3x + 2 = 70

Û 5x + 10 = 70

Û 5x = 60

Û x = 12

Vậy tập nghiệm của phương trình là S = {12}.

c) (3x − 5)² − 2(9x² − 25) = 0

$\Leftrightarrow$ (3x − 5)² – 2[(3x)² – (5)²] = 0

$\Leftrightarrow$ (3x − 5)² – 2(3x – 5)(3x + 5) = 0

$\Leftrightarrow$ (3x – 5)[3x – 5 – 2(3x + 5)] = 0

$\Leftrightarrow$ (3x – 5)(3x – 5 – 6x – 10) = 0

$\Leftrightarrow$ (3x – 5)(– 3x – 15) = 0

$\Leftrightarrow [\begin{array}{l} 3 x - 5 = 0 \\ - 3 x - 15 = 0 \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{5}{3} \\ x = - 5 \end{array}$

Vậy tập nghiệm của phương trình là

S = \{- 5; \frac{5}{3}\}

d) $\frac{x + 1}{x - 2}$ − $\frac{5}{x + 2}$ = $\frac{- 12}{x^{2} - 4}$ + 1

ĐKXĐ: $\{\begin{cases} x - 2 \neq 0 \\ x + 2 \neq 0 \\ x^{2} - 4 \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x - 2 \neq 0 \\ x + 2 \neq 0 \\ (x + 2) (x - 2) \neq 0 \end{cases}$

Phương trình đã cho tương đương với:

$\frac{x + 1}{x - 2} - \frac{5}{x + 2} = \frac{- 12}{(x + 2) (x - 2)} + 1 \Leftrightarrow \frac{(x + 1) (x + 2)}{(x - 2) (x + 2)} - \frac{5. (x - 2)}{(x + 2) (x - 2)} = \frac{- 12}{(x - 2) (x + 2)} + \frac{(x - 2) (x + 2)}{(x - 2) (x + 2)}$

Þ (x + 2)(x + 1) – 5(x – 2) = −12 + (x + 2)(x – 2)

Û (x + 2)(x + 1) – (x + 2)(x – 2) – 5(x – 2) + 12 = 0

Û (x + 2)[x + 1 – (x – 2)] – 5x + 10 + 12 = 0

Û (x + 2)(x + 1 – x + 2) – 5x + 22 = 0

Û 3(x + 2) – 5x + 22 = 0

Û 3x + 6 – 5x + 22 = 0

Û – 2x + 28 = 0

Û 2x = 28

$\Leftrightarrow$ x = 14

Vậy tập nghiệm của phương trình là S = {14}.

Câu 2:

Chứng tỏ rằng x = −5 là nghiệm của phương trình −3x + 3 = 18.

Xem đáp án

Thay x = −5 vào phương trình −3x + 3 = 18 ta được:

−3. (−5) + 3 = 18

18 = 18 (luôn đúng)

Vậy x = −5 là nghiệm của phương trình −3x + 3 = 18.

Câu 3:

Giải bài toán bằng cách lập phương trình
Một ô tô đi từ A đến B với vận tốc 40 km/h. Lúc về vẫn trên con đường đấy ô tô đi từ B đến A với vận tốc 50 km/h, vì vậy thời gian về ít hơn thời gian đi là 30 phút. Tính chiều dài quãng đường AB.

Xem đáp án

Gọi s (km) là chiều dài quãng đường AB (s > 0)

Thời gian ô tô đi từ A đến B là: $\frac{s}{40}$ (giờ)

Thời gian ô tô đi từ B đến A là: $\frac{s}{50}$ (giờ)

Đổi 30 phút = $\frac{1}{2}$ giờ.

Theo đề bài, thời gian về ít hơn thời gian đi là 30 phút nên ta có phương trình:

$\frac{s}{40}$ − $\frac{s}{50}$ = $\frac{1}{2}$

<=> $\frac{5 s}{200}$ − $\frac{4 s}{200}$ = $\frac{100}{200}$

<=> 5s – 4s = 100

<=> s = 100 (thỏa mãn)

Vậy quãng đường AB dài 100 km.

Câu 4:

Cho DABC vuông tại A, đường cao AH.

a) Chứng minh DABC đồng dạng DHBA và AB. AH = BH. AC.

b) Tia phân giác của $\hat{A B C}$ cắt AH tại I. Biết BH = 3 cm, AB = 5 cm. Tính AI, HI.
c) Tia phân giác góc HAC cắt BC tại K. Chứng minh IK // AC.

Xem đáp án

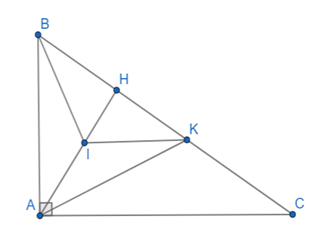
Cho ABC vuông tại A, đường cao AH. a)Chứng minh ABC đồng dạng HBA và AB. AH = BH. AC. (ảnh 1)

a) Vì DABC vuông tại A nên $\hat{B A C} = 90^{o}$ .

Mà AH là đường cao DABC hay AH ^ BC nên $\hat{A H B} = 90^{o}$ .

Do đó $\hat{B A C}$ = $\hat{A H B}$ .

Xét DABC và DHBA có:

$\hat{B A C}$ = $\hat{A H B}$ (cmt)

$\hat{B}$ là góc chung.

Do đó DABC $∽$ DHBA (g.g)

Suy ra $\frac{A B}{H B}$ = $\frac{A C}{A H}$

Vậy AB. AH = AC. HB (đpcm)

b) Xét DAHB vuông tại H, ta có:

AB² = AH² + HB² (định lý Py-ta-go)

=> AH²= AB²− HB²= 25 − 9 = 16

=> AH = 4 (cm).

Vì BI là tia phân giác của $\hat{A B C}$

=> $\frac{I A}{I H}$ = $\frac{A B}{B H}$ (tính chất đường phân giác trong tam giác)

=> $\frac{A H - H I}{I H}$ = $\frac{A B}{B H}$ = $\frac{5}{3}$

<=> $\frac{A H}{I H}$ − 1 = $\frac{5}{3}$

<=> $\frac{4}{I H} = \frac{8}{3}$

=> IH = $\frac{12}{8}$ = 1,5 (cm)

Ta có: AI = AH − IH = 4 − 1,5 = 2,5 (cm)

Vậy AI = 2,5 cm; HI = 1,5 cm.

c) Xét DABH và DCAH có:

$\hat{A H B} = \hat{A H C} = 90^{o}$

$\hat{A B H} = \hat{C A H}$ (cùng phụ $\hat{B A H}$ )

Do đó DABH DCAH (g.g)

Suy ra $\frac{A H}{B H} = \frac{H C}{A H}$ .

Suy ra AH² = BH. HC

<=>16 = 3. HC

=> HC = $\frac{16}{3}$

=> BC = $\frac{16}{3}$ + 3 = $\frac{25}{3}$ (cm)

+ AC² = BC²− AB²

=> AC² = ${(\frac{25}{3})}^{2}$ − 5²= $\frac{400}{9}$

=> AC = $\frac{20}{3}$ (cm).

Xét DHAC có AK là tia phân giác của $\hat{H A C}$ nên:

$\frac{K H}{K C}$ = $\frac{A H}{A C}$ = $\frac{3}{5}$

Mà $\frac{H I}{I A}$ = $\frac{1, 5}{2, 5}$ = $\frac{3}{5}$

Suy ra $\frac{H I}{I A}$ = $\frac{K H}{K C}$

Do đó IK // AC (định lý Ta-let đảo) (đpcm).

Câu 5:

Tìm giá trị nhỏ nhất của Q = $\frac{5 x^{2} - 24 x + 29}{x^{2} - 4 x + 4}$ với x ≠ 2.

Xem đáp án

Q = $\frac{5 x^{2} - 24 x + 29}{x^{2} - 4 x + 4} = \frac{5. (x^{2} - 4 x + 4) - 4 x + 9}{x^{2} - 4 x + 4}$

= $5 + \frac{- 4 x + 9}{x^{2} - 4 x + 4} = 5 + \frac{- 4. (x - 2) + 1}{{(x - 2)}^{2}}$

= $5 - \frac{4}{x - 2} + \frac{1}{{(x - 2)}^{2}}$

Đặt t = $\frac{1}{x - 2}$ => Q = t²− 4t + 5

= t²− 4t + 4 + 1 = (t − 2)² + 1

Vì (t − 2)² ≥ 0 nên Q = (t − 2)² + 1 ≥ 1

Do đó giá trị nhỏ nhất của Q bằng 1 khi t = 2. Khi đó:

$\frac{1}{x - 2}$ = 2

=> 2x − 4 = 1

Û x = $\frac{5}{2}$

Vậy giá trị nhỏ nhất của Q bằng 1 khi x = $\frac{5}{2}$ .

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Top 12 Đề kiểm tra Toán 8 Học Kì 2 Chương 3 Đại Số có đáp án, cực hay

( 9.9 K lượt thi )

Top 8 Đề kiểm tra Toán 8 Học Kì 2 Chương 4 Đại Số có đáp án, cực hay

( 4.8 K lượt thi )

Top 9 Đề kiểm tra Toán 8 Học Kì 2 Chương 3 Hình học có đáp án, cực hay

( 5.6 K lượt thi )

Top 5 Đề kiểm tra Toán 8 Chương 4 Học Kì 2 Hình học có đáp án, cực hay

( 3.3 K lượt thi )

Top 4 Đề thi Toán 8 Học kì 2 có đáp án, cực sát đề chính thức

( 4.5 K lượt thi )

Top 11 Đề kiểm tra Đại số Toán 8 Học Kì 1 Chương 1 có đáp án, cực hay

( 7.6 K lượt thi )

Top 8 Đề kiểm tra Toán 8 Học Kì 1 Chương 1 Hình học có đáp án, cực hay

( 7.4 K lượt thi )

Đề thi Toán lớp 8 Học kì 1 năm 2020 - 2021 cực hay, có đáp án

( 6.3 K lượt thi )

Top 8 Đề kiểm tra Đại Số Toán 8 Học Kì 1 Chương 2 có đáp án, cực hay

( 5.5 K lượt thi )

Top 4 Đề thi Toán 8 Học kì 1 có đáp án, cực sát đề chính thức

( 5.4 K lượt thi )

Đánh giá trung bình

Thi Online Đề kiểm tra giữa kì 2 Toán 8 có đáp án ( Mới nhất)