Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)

Thi Online Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)

Đề kiểm tra cuối kỳ 2 Toán 8 có đáp án ( Mới nhất)_ đề 11

8318 lượt thi
5 câu hỏi
45 phút

BẮT ĐẦU LÀM BÀI

Câu 1:

Giải các phương trình sau:

a) 6x + 7 = 3x – 2;

b) x² – 25 = 8(5 – x);

c) $\frac{x - 2}{x + 2} - \frac{2 (x - 11)}{x^{2} - 4} = \frac{3}{x - 2}$ .

Xem đáp án

a) 6x + 7 = 3x – 2

Û 6x – 3x = – 2 – 7

Û 3x = – 9

Û x = – 3

Vậy tập nghiệm của phương trình đã cho là S = {– 3};

b) x² – 25 = 8.(5 – x)

Û x² – 25 – 8.(5 – x) = 0

Û (x + 5)(x – 5) + 8(x – 5) = 0

Û (x – 5)(x + 5 + 8) = 0

Û (x – 5)(x + 13)= 0

\Leftrightarrow [\begin{matrix} x - 5 = 0 \\ x + 13 = 0 \end{matrix}

\Leftrightarrow [\begin{matrix} x = 5 \\ x = - 13 \end{matrix}

Vậy tập nghiệm của phương trình đã cho là S = {–13; 5};

c) $\frac{x - 2}{x + 2} - \frac{2 (x - 11)}{x^{2} - 4} = \frac{3}{x - 2}$

Điều kiện xác định của phương trình:

\{\begin{cases} x + 2 \neq 0 \\ x^{2} - 4 \neq 0 \\ x - 2 \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x + 2 \neq 0 \\ (x - 2) (x + 2) \neq 0 \\ x - 2 \neq 0 \end{cases}

\Leftrightarrow \{\begin{matrix} x + 2 \neq 0 \\ x - 2 \neq 0 \end{matrix} \Leftrightarrow \{\begin{cases} x \neq - 2 \\ x \neq 2 \end{cases}

Với x ≠ 2, x ≠ –2 ta có:

\frac{x - 2}{x + 2} - \frac{2 (x - 11)}{x^{2} - 4} = \frac{3}{x - 2}

\Leftrightarrow \frac{(x - 2) (x - 2)}{(x + 2) (x - 2)} - \frac{2 (x - 11)}{(x + 2) (x - 2)} = \frac{3 (x + 2)}{(x - 2) (x + 2)}

Þ (x – 2)(x – 2) – 2(x – 11) = 3(x + 2)

Û x² – 4x + 4 – 2x + 22 = 3x + 6

Û x² – 4x – 2x – 3x + 4 + 22 – 6 = 0

Û x² – 9x + 20 = 0

Û x² – 5x – 4x + 20 = 0

Û (x² – 5x) – (4x – 20) = 0

Û x(x – 5) – 4 (x – 5) = 0

Û (x – 5)(x – 4) = 0

\Leftrightarrow [\begin{matrix} x - 5 = 0 \\ x - 4 = 0 \end{matrix}

$\Leftrightarrow [\begin{matrix} x = 5 \\ x = 4 \end{matrix}$ (thõa mãn điều kiện)

Vậy tập nghiệm của phương trình đã cho là S = {4; 5}.

Câu 2:

Giải các bất phương trình sau và biểu diễn tập nghiệm trên trục số:

a) 3(x – 5) < x + 7;

b) $\frac{x + 2}{3} - \frac{x - 1}{2} > \frac{x + 1}{4}$ .

Xem đáp án

a) 3(x – 5) < x + 7

Û 3x – 15 – x – 7 < 0

Û 2x – 22 < 0

Û 2x < 22

Û x < $\frac{22}{2}$

Û x < 11

Vậy bất phương trình đã cho có tập nghiệm S = {x| x < 11};

b) $\frac{x + 2}{3} - \frac{x - 1}{2} > \frac{x + 1}{4}$

$\Leftrightarrow \frac{4 (x + 2)}{4.3} - \frac{6 (x - 1)}{6.2} > \frac{3 (x + 1)}{3.4}$

$\Leftrightarrow \frac{4 x + 8}{12} - \frac{6 x - 1}{12} > \frac{3 x + 3}{12}$

Û 4x + 8 – (6x – 1) > 3x + 3

Û 4x + 8 – 6x + 6 – 3x – 3 > 0

Û (4x – 6x – 3x) + (8 + 6 – 3) > 0

Û – 5x + 11 > 0

Û –5x > –11

Û x < $\frac{11}{5}$

Vậy bất phương trình đã cho có tập nghiệm là S = {x| $x < \frac{11}{5}$ }.

Câu 3:

Ông Tư có mảnh vườn trồng xoài hình chữ nhật với chiều dài hơn chiều rộng 20 m. Nếu tăng chiều rộng thêm 10 m và giảm chiều dài 5 m thì diện tích tăng thêm 350 m².

a) Tính diện tích của mảnh vườn nhà ông Tư.

b) Theo tính toán của ông Tư, vườn xoài của ông nếu đạt năng suất thì phải thu hoạch được ít nhất 700 kg trở lên. Năm vừa qua Ông Tư hoạch xoài và bán 80 % số xoài trong vườn cho lái buôn được 20.000.000 đồng với giá 40.000 đồng/ 1 kg. Phần còn lại ông để ăn và cho bà con hàng xóm. Hỏi vườn xoài của ông thu được tất cả bao nhiêu kilogam và đã đạt được năng suất như ông mong muốn chưa?

Xem đáp án

a) Gọi x (m, x > 0) là chiều dài ban đầu của mảnh vườn hình chữ nhật nhà ông Tư.

Vì chiều dài hơn chiều rộng 20 m nên chiều rộng ban đầu của mảnh vườn nhà ông Tư là x – 20 (m, x > 20).

Diện tích mảnh vườn hình chữ nhật nhà ông Tư là x(x – 20) m².

Khi tăng chiều rộng lên 10 m thì chiều rộng mới là x – 20 + 10 = x – 10 (m)

Khi chiều dài giảm đi 5 m thì chiều dài mới là x – 5 (m).

Diện tích của mảnh vườn hình chữ nhật sau khi thay đổi chiều rộng và chiều dài là

(x – 10).(x – 5) (m²).

Mặc khác diện tích mảnh vườn hình chữ nhật sau thay đổi chiều rộng và chiều dài tăng thêm 350 m² nên ta có phương trình sau:

(x – 10).(x – 5) – x(x – 20) = 350

Û x² – 5x – 10x + 50 – x² + 20x = 350

Û x²– x² – 5x – 10x + 20x + 50 – 350 = 0

Û 5x – 300 = 0

Û x = 300 : 5

Û x = 60 (thõa mãn điều kiện)

Chiều dài ban đầu của mảnh vườn hình chữ nhật nhà ông Tư là 60 m.

Suy ra, chiều rộng ban đầu của mảnh vườn nhà ông Tư là 60 – 20 = 40 m.

Vậy diện tích mảnh vườn hình chữ nhật nhà ông Tư là 60.40 = 2400 m².

b) Gọi y (kg, y > 0) là số kilogam xoài mà ông Tư thu hoạch được trong năm vừa qua.

Theo đề ông Tư bán 80 % số xoài đã thu hoạch nên số kiogam xoài ông Tư đã bán là y.80% = 0,8y (kg).

Mỗi cân xoài ông Tư bán cho lái buôn với giá 40 000 đồng và được 20 000 000 đồng nên ta có phương trình:

0,8y.40 000 = 20 000 000

Û 32 000.y = 20 000 000

Û y = 20 000 000 : 32 000

Û y = 625 (thõa mãn điều kiện)

Sản lượng xoài mà ông Tư thu hoạch được trong năm vừa rồi là 625 kg.

Vì theo tính toán của ông Tư, vườn xoài của ông nếu đạt năng suất thì phải thu hoạch được ít nhất 700 kg trở lên nhưng chỉ thu hoạch được 625 kg nên chưa đạt được năng suất như ông mong muốn.

Câu 4:

Nhà bạn An có một bể cá hình hộp chữ nhật với kích thước như sau: chiều dài đáy bể là 1,5 m; chiều rộng đáy bể là 1,2 m và chiều cao của bể là 0,9 m. Ba bạn An đổ nước vào bể cá sao cho khoảng cách từ mặt nước đến miệng bể cá là 0,2 m. Hỏi ba bạn An đã đổ bao nhiêu lít nước vào bể cá?

(Biết thể tích của hình hộp chữ nhật được tính theo công thức: V = S.h, trong đó:

S là điện tích đáy; h là chiều cao).

Xem đáp án

Gọi x (m, x > 0) là chiều cao phần nước mà ba của An đã đổ vào bể cá.

Theo đề bể cá cao 0,9 m và khoảng cách từ từ mặt nước đến miệng bể cá là 0,2 m nên ta được phương trình sau:

0,9 – x = 0,2

Û x = 0,9 – 0,2

Û x = 0,7 ( thõa mãn điều kiện)

Chiều cao phần nước mà ba của An đổ vào bể cá là 0,7 m.

Diện tích đáy của bể cá là 1,5.1,2 = 1,8 (m²)

Suy ra, thể tích của phần nước trong bể cá mà ba của An đổ vào là:

1,8.0,7 = 1,26 (m³) = 1 260 (l)

Vậy ba của An đã đổ vào bể cá l 260 lít nước.

Câu 5:

Cho ABC có ba góc nhọn (AB < AC), vẽ các đường cao BD và CE.

a) Chứng minh ∆ABD ᔕ ∆ACE;

b) Chứng minh $\hat{A B C} + \hat{E D C} = 180^{0}$ ;

c) Gọi M, N lần lượt là trung điểm của đoạn thẳng BD và CE. Vẽ AK là phân giác của $\hat{M A N}$ (K Î BC). Chứng minh KB.AC = KC.AB.

Xem đáp án

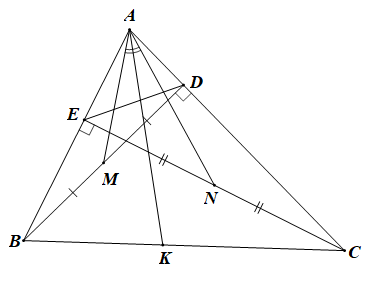
a) Xét ∆ABD và ∆ACE có:

$\hat{B A C}$ chung,

$\hat{A D B} = \hat{A E C} = 90 °$ (gt)

Suy ra ∆ABD ᔕ ∆ACE (g.g)

b) Vì ∆ABD ᔕ ∆ACE (câu a)

$\Rightarrow \frac{A D}{A E} = \frac{A B}{A C}$ (các cặp cạnh tương ứng tỉ lệ)

Xét ∆AED và ∆ACB có

$\frac{A D}{A E} = \frac{A B}{A C}$ ( chứng minh trên)

$\hat{B A C}$ chung,

Suy ra, ∆AED ᔕ ∆ACB (c.g.c)

$\Rightarrow \hat{A D E} = \hat{A B C}$ (hai góc tương ứng)

Mặc khác: $\hat{A D E} + \hat{E D C} = 180 °$ (hai góc kề bù)

Do đó $\hat{A D E} + \hat{E D C} = \hat{A B C} + \hat{E D C} = 180 °$ .

Vậy $\hat{A B C} + \hat{E D C} = 180 ° .$

c) Vì ∆ABD ᔕ ∆ACE (câu a)

$\Rightarrow \frac{A B}{A C} = \frac{B D}{C E}$ (tỉ số đồng dạng)

Mà M là trung điểm của BD, N là trung điểm của CE (giả thiết)

Nên ta có: BD = 2BM và CE = 2CN

\Rightarrow \frac{A B}{A C} = \frac{B D}{C E} = \frac{2 B M}{2 C N} = \frac{B M}{C N}

Xét DABM và DACN có:

$\frac{A B}{A C} = \frac{B M}{C N}$ (chứng minh trên),

$\hat{A B M} = \hat{A C N}$ (do cùng phụ với $\hat{B A C}$ )

Þ DABM ᔕ DACN (c.g.c)

$\Rightarrow \hat{B A M} = \hat{C A N}$ (hai góc tương ứng)

Lại có AK là tia phân giác của $\hat{M A N}$ (giả thiết)

$\Rightarrow \hat{M A K} = \hat{N A K}$ (tính chất tia phân giác của một góc)

Do đó: $\hat{B A M} + \hat{M A K} = \hat{C A N} + \hat{N A K}$

Hay $\hat{B A K} = \hat{K A C}$

Þ AK là tia phân giác của $\hat{B A C}$

Theo tính chất tia phân giác của tam giác ta có:

$\frac{A B}{A C} = \frac{K B}{K C}$

Þ KB.AC = KC.AB (điều phải chứng minh).

Vậy KB.AC = KC.AB.

Bắt đầu thi để xem toàn bộ câu hỏi trong đề

Bài thi liên quan:

Các bài thi hot trong chương:

Top 12 Đề kiểm tra Toán 8 Học Kì 2 Chương 3 Đại Số có đáp án, cực hay

( 9.9 K lượt thi )

Top 8 Đề kiểm tra Toán 8 Học Kì 2 Chương 4 Đại Số có đáp án, cực hay

( 4.8 K lượt thi )

Top 9 Đề kiểm tra Toán 8 Học Kì 2 Chương 3 Hình học có đáp án, cực hay

( 5.6 K lượt thi )

Top 5 Đề kiểm tra Toán 8 Chương 4 Học Kì 2 Hình học có đáp án, cực hay

( 3.3 K lượt thi )

Top 4 Đề thi Toán 8 Học kì 2 có đáp án, cực sát đề chính thức

( 4.6 K lượt thi )

Top 11 Đề kiểm tra Đại số Toán 8 Học Kì 1 Chương 1 có đáp án, cực hay

( 7.6 K lượt thi )

Top 8 Đề kiểm tra Toán 8 Học Kì 1 Chương 1 Hình học có đáp án, cực hay

( 7.4 K lượt thi )

Đề thi Toán lớp 8 Học kì 1 năm 2020 - 2021 cực hay, có đáp án

( 6.3 K lượt thi )

Top 8 Đề kiểm tra Đại Số Toán 8 Học Kì 1 Chương 2 có đáp án, cực hay

( 5.5 K lượt thi )

Top 4 Đề thi Toán 8 Học kì 1 có đáp án, cực sát đề chính thức

( 5.4 K lượt thi )

Đánh giá trung bình

100%

Nhận xét

11 tháng trước

Hoàng văn anh

Thi Online Đề kiểm tra cuối kì 2 Toán 8 có đáp án ( Mới nhất)