Dạng 5. Bài nâng cao phát triển tư duy có đáp án

43 người thi tuần này 4.6 4.2 K lượt thi 19 câu hỏi 45 phút

Câu 1

Cho tam giác ABC cân tại A. Gọi D, E,F lần lượt là trung điểm của các cạnh BC, AB, AC. Chứng minh: tứ giác AEDF là hình thoi.

Xem đáp án

Lời giải

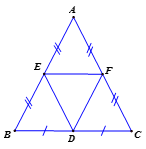
Cho tam giác ABC cân tại A. Gọi D, E,F lần lượt là trung điểm của các cạnh BC, AB, AC. Chứng minh: tứ giác AEDF là hình thoi. (ảnh 1)

Cách 1: Vì D, Elà trung điểm của các cạnh BC, AB => DE là đường trung bình của $Δ A B C$

=> $D E = \frac{1}{2} A C$ (1)

Vì D, F là trung điểm của các cạnh BC, AC, => DF là đường trung bình của $Δ A B C$

=> $D F = \frac{1}{2} A B$ (2)

Vì E, F là trung điểm của các cạnh AB, AC => $A E = \frac{1}{2} A B, A F = \frac{1}{2} A C$ (3)

Tam giác ABC cân tại A => AB = AC (4)

Từ (1), (2), (3), (4) => AE = ED = DF = FA.

Tứ giác AEDFcó AE = ED = DF = FA => AEDF là hình thoi.

Cách 2: Vì D, F là trung điểm của các cạnh BC, AC => DF là đường trung bình của $Δ A B C$

=> $D F / / A B$ và $D F = \frac{1}{2} A B$

Mà AB = AE và A, E, B thẳng hàng

Tứ giác AEDF có $\{\begin{cases} D F / / A E \\ D F = A E \end{cases} \Rightarrow E A D F$ là hình bình hành.

Hình bình hành AEDF có $A E = A F (= \frac{1}{2} A B = \frac{1}{2} A C) \Rightarrow A E D F$ là hình thoi.

Câu 2

Cho tam giác ABC cân tại A. Trên nửa mặt phẳng không chứa Acó bờ là đường thẳng chứa cạnh BC, vẽ tia Bx // AC và tia Cy // AB. Gọi D là giao điểm của hai tia Bx và Cy. Chứng minh: tứ giác ACDB là hình thoi.

Xem đáp án

Lời giải

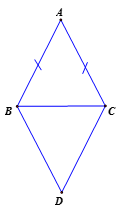
Cho tam giác ABC cân tại A. Trên nửa mặt phẳng không chứa Acó bờ là đường thẳng chứa cạnh BC, vẽ tia Bx // AC và tia Cy // AB. (ảnh 1)

Vì $\{\begin{cases} C y / / A B \\ B x / / A C \end{cases} \Rightarrow \{\begin{cases} C D / / A B \\ B D / / A C \end{cases}$

Tứ giác ACDB có $\{\begin{cases} C D / / A B \\ B D / / A C \end{cases} \Rightarrow A C D B$ là hình bình hành.

Hình bình hành ACDB có AB = AC (tam giác ABC cân tại A) => AEDF là hình thoi.

Câu 3

Cho $△$ ABC cân tại B có đường cao BE. Trên tia đối của tia EB lấy điểm D sao cho ED = EB. Chứng minh: tứ giác ABCD là hình thoi.

Xem đáp án

Lời giải

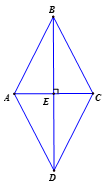
Cho ABC cân tại B có đường cao BE. Trên tia đối của tia EB lấy điểm D sao cho ED = EB. Chứng minh: tứ giác ABCD là hình thoi. (ảnh 1)

Vì $△$ ABC cân tại B có đường cao BE => BE là đường trung tuyến

=> EA = EC (1)

Ta có : EB = ED (gt) (2)

Từ (1) và (2) => ABCD là hình bình hành.

Vì BE là đường cao của $△$ ABC => $B E ⊥ A C$

Hình bình hành ABCD có $B E ⊥ A C$ => ABCD là hình thoi.

Câu 4

Cho $Δ A B C$ cân tại B. Đường thẳng qua C song song với AB cắt tia phân giác của $\hat{A B C}$ tại D. Chứng minh: tứ giác ABCD là hình thoi.

Xem đáp án

Lời giải

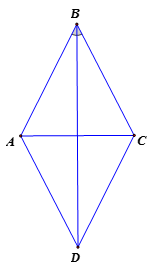
Cho ABC cân tại B. Đường thẳng qua C song song với AB cắt tia phân giác của góc ABC tại D. Chứng minh: tứ giác ABCD là hình thoi. (ảnh 1)

Vì $C D / / A B \Rightarrow \hat{A B D} = \hat{B D C}$ (so le trong) (1)

Vì BD là phân giác của $\hat{A B C} \Rightarrow \hat{A B D} = \hat{D B C}$ (2)

Từ (1) và (2) => $\hat{B D C} = \hat{D B C} \Rightarrow Δ B C D$ cân tại $D \Rightarrow C B = C D$ (3)

Vì $△$ ABC cân tại B => CB = AB (4)

Từ (3) và (4) => AB = CD.

Tứ giác ABCD có $\{\begin{cases} A B = C D \\ A B / / C D \end{cases} \Rightarrow A B C D$ là hình bình hành.

Cách 1: Hình bình hành ABCD có DB là phân giác của $\hat{A B C} \Rightarrow$ => ABCD là hình thoi.

Cách 2: Hình bình hành ABCD có CB = AB => ABCD là hình thoi.

Câu 5

Cho hình bình hành ABCD có $A D ⊥ A C$ . Gọi M, N theo thứ tự là trung điểm của AB, CD . Chứng minh tứ giác AMCN là hình thoi.

Xem đáp án

Lời giải

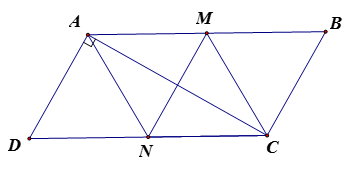
Cho hình bình hành ABCD có AD vuông AC. Gọi M, N theo thứ tự là trung điểm của AB, CD . Chứng minh tứ giác AMCN là hình thoi. (ảnh 1)

Vì ABCD là hình bình hành => $\{\begin{cases} A B / / C D \\ A D / / B C \end{cases}$

Tứ giác AMCN có $\{\begin{cases} A M = C N \\ A M / / C N \end{cases} \Rightarrow A M C N$ là hình bình hành (1)

Tứ giác AMND có $\{\begin{cases} A M = D N \\ A M / / D N \end{cases} \Rightarrow A M N D$ là hình bình hành

=> AD // MN, mà $A D ⊥ A C \Rightarrow M N ⊥ A C$ (2)

Từ (1) và (2) => AMCN là hình thoi.

Câu 6