Bộ 20 đề thi giữa kì 1 Toán 12 năm 2022-2023 có đáp án (Đề 5)
28 người thi tuần này 5.0 12.6 K lượt thi 50 câu hỏi 90 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Danh sách câu hỏi:
Câu 1/50
A. \(( - 1\,;\,1)\).
B. \((0\,;\, + \infty )\).
C. \(\mathbb{R}\).
D. \(( - \infty \,;\,0)\).
Lời giải
Lời giải
Chọn B
Tập xác định \(D = \mathbb{R}\).
Ta có \(y' = 4{x^3} + 4x = 4x({x^2} + 1)\); \(y' = 0 \Leftrightarrow x = 0\).
Bảng biến thiên
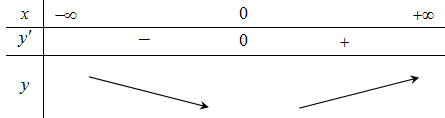
Hàm số đồng biến trên khoảng \((0\,;\, + \infty )\).
Câu 2/50
A. \(\left( {1;4} \right).\)
B. \(\left( {0;2} \right).\)
C. \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right).\)
D. \(\left( { - \infty ;1} \right)\) và \(\left( {4; + \infty } \right).\)
Lời giải
Lời giải
Chọn B
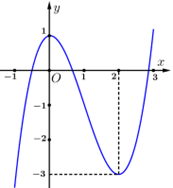
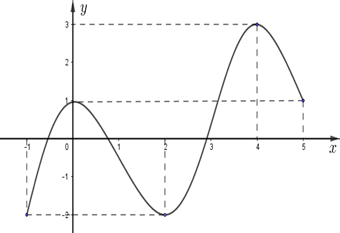
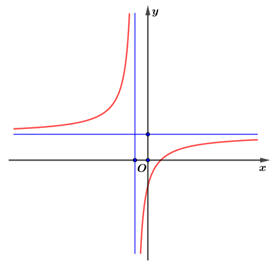
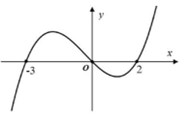
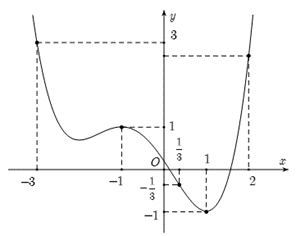
Quan sát bảng đồ thị, ta thấy hàm số nghịch biến trên các khoảng \(\left( {0;2} \right).\)
Nên chọn đáp án
Câu 3/50
A. Nghịch biến trên khoảng \(\left( {3; + \infty } \right)\).
B. Đồng biến trên khoảng \(\left( {0;6} \right)\).
C. Nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).
D. Đồng biến trên khoảng \(\left( { - 1;3} \right)\).
Lời giải
Lời giải
Chọn B
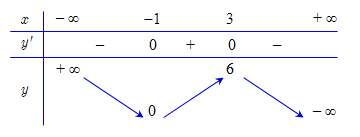
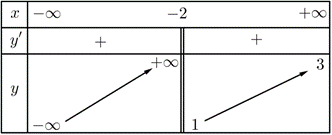
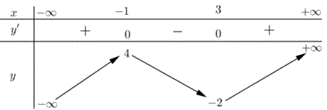
Từ bảng biến thiên ta thấy \(y' < 0\)với mọi \(x > 3\), suy ra hàm số nghịch biến trên khoảng \(\left( {3;6} \right)\), do đó hàm số không thể đồng biến trên khoảng \(\left( {0;6} \right)\).
Câu 4/50
A. Nhận điểm \(x = 6\)làm điểm cực đại.
B. Nhận điểm \(x = 6\)làm điểm cực tiểu.
C. Nhận điểm \(x = 0\)làm điểm cực đại.
D. Nhận điểm \(x = 0\)làm điểm cực tiểu.
Lời giải
Lời giải
Chọn B
\(f'\left( x \right) = 4{x^3} - 24{x^2} = 4{x^2}\left( {x - 6} \right)\) ; \(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 6\end{array} \right.\).
Bảng biến thiên
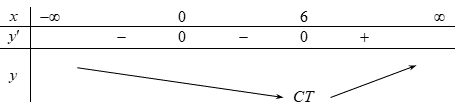
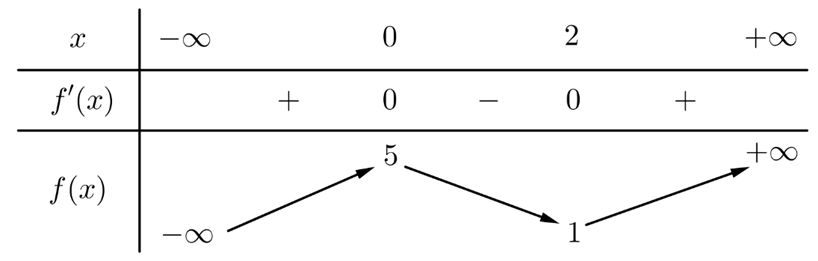
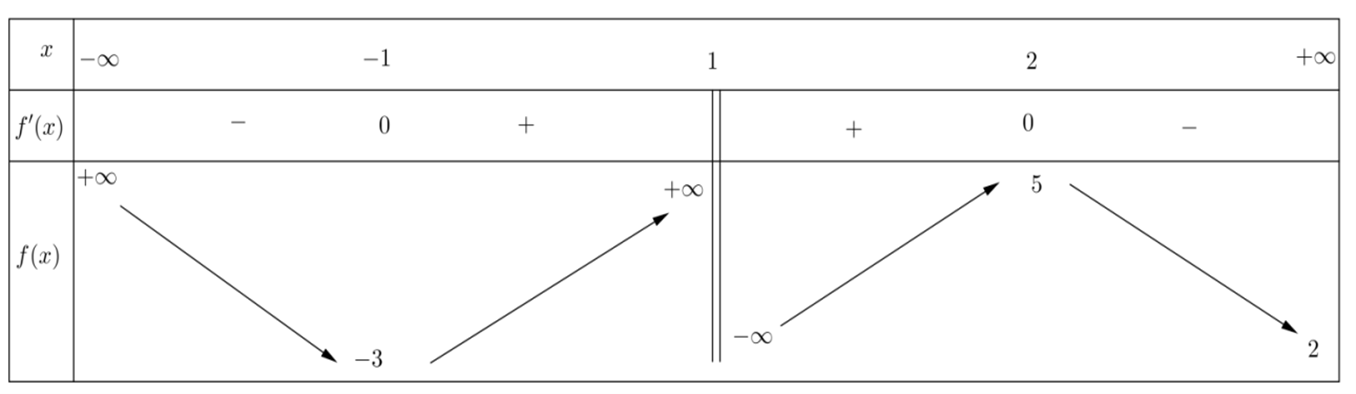
Từ bảng biến thiên ta thấy hàm số nhận điểm \(x = 6\)làm điểm cực tiểu.
Câu 5/50
A. \(M\left( { - 1; - 4} \right)\).
B. \(N\left( {0; - 3} \right)\)
C. \(x = - 1\).
D. \(x = 0\).
Lời giải
Lời giải
Chọn B
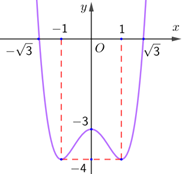
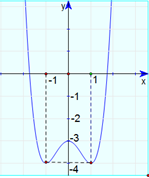
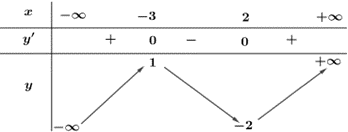
Dựa vào đồ thị của hàm số, điểm cực đại của đồ thị hàm số là \(N\left( {0; - 1} \right)\).
Câu 6/50
A. Giá trị cực tiểu của hàm số bằng \(2\).
B. Hàm số đạt cực tiểu tại \(x = 1\) và đạt cực đại tại \(x = 5\).
C. Hàm số đạt cực đại tại \(x = 0\) và đạt cực tiểu tại \(x = 2\).
D. Giá trị cực đại của hàm số là \(0\).
Lời giải
Lời giải
Chọn C
Dựa vào bảng biến thiên, ta thấy hàm số có giá trị cực đại bằng \(5\) tại \(x = 0\) và có giá trị cực tiểu bằng \(1\) tại \(x = 2.\) Từ các đáp án A, B, C, D ta chọn
Câu 7/50
A. \( - 4\).
B. \(4\).
C. \(1\).
D. \( - 1\).
Lời giải
Lời giải
Chọn A
Xét hàm số \(y = {x^3} + 3{x^2} - 9x + 1\)xác định và liên tục trên đoạn \(\left[ { - 4;4} \right]\).
Ta có \(y' = 3{x^2} + 6x - 9\); \(y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1 \in \left[ { - 4;4} \right]\\x = - 3 \in \left[ { - 4;4} \right]\end{array} \right.\).
Khi đó \(y\left( { - 4} \right) = 21\), \(y\left( { - 3} \right) = 28\), \(y\left( 1 \right) = - 4\), \(y\left( 4 \right) = 77\).
Vậy giá trị nhỏ nhất của hàm số \(y = {x^3} + 3{x^2} - 9x + 1\)trên đoạn \(\left[ { - 4;4} \right]\)là \( - 4\).
Lời giải
Lời giải
Chọn C
Nhìn đồ thị của hàm số\(f(x)\) trên đoạn \(\left[ { - 1\,;5} \right]\)ta thấy:
\(M = \mathop {\max }\limits_{\left[ { - 1;5} \right]} f(x) = 3\)và \(m = \mathop {\min }\limits_{\left[ { - 1;5} \right]} f(x) = - 2\)nên \(M + m = 1\).Câu 9/50
A. \(x = 1\).
B. \(x = 0\).
C. \(y = 1\).
D. \(y = 0\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 10/50
A. \(1\).
B. \(3\).
C. \(4\).
D. \(2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 11/50
A. \(y = \frac{{x + 2}}{{1 - x}}\).
B. \(y = \frac{{x - 1}}{{x + 1}}\).
C. \(y = \frac{{x + 1}}{{x - 1}}\).
D. \(y = \frac{{2x - 1}}{{x - 1}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 12/50
A. \[4\].
B. \[2\].
C. \[3\].
D. \[1\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 13/50
A. Tồn tại một hình đa diện có số cạnh bằng số đỉnh.
B. Tồn tại một hình đa diện có số cạnh và số mặt bằng nhau.
C. Số đỉnh và số mặt của hình đa diện luôn bằng nhau.
D. Tồn tại một hình đa diện có số đỉnh và số mặt bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 15/50
A. \(\left\{ {3\,;\,4} \right\}\).
B. \(\left\{ {5\,;\,3} \right\}\).
C. \(\left\{ {4\,;\,3} \right\}\).
D. \(\left\{ {3\,;\,5} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 16/50
A. \(V = 60{a^3}\).
B. \(V = 40{a^3}\).
C. \(V = 120{a^3}\).
D. \(V = 20{a^3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 17/50
A. \[V = \frac{{{a^3}\sqrt 3 }}{{12}}\].
B. \[V = \frac{{{a^3}\sqrt 3 }}{8}\].
C. \[V = \frac{{{a^3}\sqrt 3 }}{6}\].
D. \[V = \frac{{{a^3}\sqrt 3 }}{{24}}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 18/50
A. \(10\).
B. \(7\).
C. \(3\).
D. \(21\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 19/50
A. \(84c{m^3}\).
B. \(12c{m^3}\).
C. \(28c{m^3}\).
D. \(21c{m^3}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 20/50
A. \(\left( { - \infty \,;\, - 1} \right)\).
B. \(\left( { - 1\,;\,1} \right)\).
C. \(\left( {2\,;\, + \infty } \right)\).
D. \(\left( {1\,;\,2} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Xem tiếp với tài khoản VIP
Còn 42/50 câu hỏi, đáp án và lời giải chi tiết.
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập