Bộ 25 đề thi học kì 1 Toán 12 năm 2022-2023 có đáp án (Đề 6)

✕

✨ Đăng kí VIP để truy cập không giới hạn. Đăng ký ngay

🔥 Học sinh cũng đã học

22 người thi tuần này

Đề cương ôn tập cuối kì 2 Toán 12 Kết nối tri thức cấu trúc mới (có tự luận) có đáp án - Chương IV. Nguyên hàm và tích phân

44 lượt thi x câu hỏi

49 người thi tuần này

Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Tự luận

224 lượt thi 20 câu hỏi

29 người thi tuần này

Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Phương trình mặt phẳng

204 lượt thi 29 câu hỏi

17 người thi tuần này

Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 4. Ứng dụng hình học của tích phân

192 lượt thi 24 câu hỏi

21 người thi tuần này

Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 3. Tích phân

196 lượt thi 22 câu hỏi

21 người thi tuần này

Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 2. Nguyên hàm của một số hàm số sơ cấp

196 lượt thi 22 câu hỏi

38 người thi tuần này

Đề cương ôn tập giữa kì 2 Toán 12 Cánh diều cấu trúc mới (có tự luận) có đáp án - Bài 1. Nguyên hàm

213 lượt thi 22 câu hỏi

26 người thi tuần này

Đề cương ôn tập giữa kì 2 Toán 12 Chân trời sáng tạo cấu trúc mới (có tự luận) có đáp án - Tự luận

144 lượt thi 20 câu hỏi

Danh sách câu hỏi:

Câu 1

Tập xác định của hàm số y = tan2x là

A. $D = ℝ \ \{\frac{π}{4} + k π, k \in ℤ\}$

B.

D = ℝ \ \{\frac{π}{4} + \frac{k π}{2}, k \in ℤ\}

C.

D = ℝ \ \{\frac{k π}{2}, k \in ℤ\}

D.

D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}

Lời giải

Điều kiện $\cos 2 x \neq 0 \Leftrightarrow 2 x \neq \frac{π}{2} + k 2 π, k \in ℤ \Leftrightarrow x \neq \frac{π}{4} + k π, k \in ℤ .$

TXĐ: $D = ℝ \ \{\frac{π}{4} + k π, k \in ℤ\} .$

Chọn A.

Câu 2

Tìm tập nghiệm S của bất phương trình $\log_{2} (3 x - 2) - \log_{2} (6 - 5 x) > 0.$

A. $S = (1; \frac{6}{5})$

B.

S = (\frac{2}{3}; 1)

C.

S = (1; + \infty)

D.

S = (1; \frac{6}{5}]

Lời giải

Điều kiện $\frac{2}{3} < x < \frac{6}{5} .$

$\begin{array}{l} \log_{2} (3 x - 2) - \log_{2} (6 - 5 x) > 0 \\ \Leftrightarrow \log_{2} (3 x - 2) > \log_{2} (6 - 5 x) \\ \Leftrightarrow 3 x - 2 > 6 - 5 x \Leftrightarrow x > 1 \end{array}$

Kết hợp với điều kiện ta được tập nghiệm của bất phương trình là $S = (1; \frac{6}{5}) .$

Chọn A.

Câu 3

Khối bát diện đều là khối đa diện đều loại nào?

A. $\{5; 3\}$

B.

\{3; 4\}

C.

\{4; 3\}

D.

\{3; 5\}

Lời giải

Mỗi mặt của khối bát diện đều là tam giác đều có 3 cạnh.
Mỗi đỉnh của khối bát diện đều là đỉnh chung của đúng 4 mặt.
Nên khối bát diện đều là khối đa diện đều loại $\{3; 4\} .$

Chọn B.

Câu 4

Họ nguyên hàm của hàm số $f (x) = 3^{x} + 1$ là

A. $\frac{3^{x}}{\ln 3} + C$

B.

\frac{3^{x}}{\ln 3} + x + C

C.

3^{x} + x + C

D.

3^{x} . \ln x + x + C

Lời giải

$\int f (x) d x = \int (3^{x} + 1) d x = \frac{3^{x}}{\ln 3} + x + C .$

Chọn B.

Câu 5

Tìm giá trị nhỏ nhất của hàm số $f (x) = x - 5 + \frac{1}{x}$ trên khoảng $(0; + \infty)$

A. $\min_{(0; + \infty)} f (x) = - 3$

B.

\min_{(0; + \infty)} f (x) = - 5

C.

\min_{(0; + \infty)} f (x) = 2

D.

\min_{(0; + \infty)} f (x) = 3

Lời giải

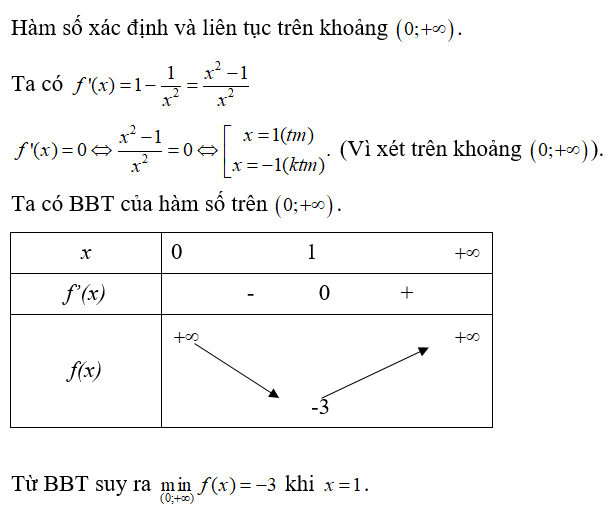
Tìm giá trị nhỏ nhất của hàm số f(x)= x -5 +1/x trên khoảng (0; dương vô cùng) (ảnh 1)

Chọn A.

Câu 6

Giải phương trình $2 \log_{4} x + \log_{2} (x - 3) = 2.$

A. x = 16

B. x = 1

C. x = 4

D. x = 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 7

$\lim_{x \to - \infty} \frac{x}{x^{2} + 1}$ bằng

A. $- \infty$

B. 1

C.

+ \infty

D. 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 8

Một vật chuyển động vận tốc tăng liên tục được biểu diễn bằng đồ thị là đường cong parabol có hình bên. Biết rằng sau 10s thì vật đó đạt đến vận tốc cao nhất 50m/s và bắt đầu giảm tốc. Hỏi từ lúc bắt đầu đến lúc đạt vận tốc cao nhất thì vật đó đã đi được quãng đường bao nhiêu mét?

A. 300m

B.

\frac{1400}{3}

m

C.

\frac{1100}{3}

m

D.

\frac{1000}{3}

m

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 9

Cho hình trụ có bán kính đáy bằng 2 cm. Một mặt phẳng đi qua trục của hình trụ và cắt hình trụ theo thiết diện là hình vuông. Tính thể tích khối trụ đã cho.

A. $8 π$ cm3

B.

16 π

cm3

C.

\frac{16 π}{3}

cm3

D. 16 cm3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 10

Đồ thị hàm số $y = 1 - \frac{x}{x - 1}$ có bao nhiêu đường tiệm cận?

A. 3

B. 0

C. 1

D. 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 11

Hàm số $y = x^{3} - 3 x$ đồng biến trên khoảng nào sau?

A. (-2;0)

B. (0;1)

C. (-2018;-2)

D. (-1;0)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 12

Hình trụ có bao nhiêu mặt phẳng đối xứng?

A. Vô số

B. 2

C. 0

D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 13

Đạo hàm của hàm số $y = 8^{x^{2} + 1}$

A. $y' = 2 x {.8}^{x^{2}}$

B.

y' = 2 x (x^{2} + 1) {.8}^{x^{2}} \ln 8

C.

y' = (x^{2} + 1) {.8}^{x^{2}}

D.

y' = 6 x {.8}^{x^{2} + 1} \ln 2

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 14

Thể tích khối lăng trụ có chiều cao h diện tích đáy B là

A. $V = \frac{1}{2} B h$

B.

V = \frac{1}{3} B h

C. V = Bh

D.

V = \frac{1}{6} B h

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 15

Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây?

A. $y = \frac{2 x + 1}{x - 1}$

B.

y = \frac{2 x - 1}{x + 1}

C.

y = \frac{x - 1}{2 x + 1}

D.

y = \frac{x + 1}{2 x - 1}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 16

Một nhóm có 6 học sinh gồm 4 nam và 2 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh trong đó có cả nam và nữ.

A. 14

B. 15

C. 17

D. 16

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 17

Cho hàm số y = (x) có bảng biến thiên như hình vẽ sau:

Hàm số y = f(x) đạt cực tiểu tại điểm nào trong các điểm sau?

A. x = 5

B. x = 0

C. x = 2

D. x = 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 18

Tìm tập hợp điểm biểu diễn của số phức z thỏa mãn $|z + 1 - 2 i| = 3$

A. Đường tròn tâm I(-1;2), bán kính r = 9

B. Đường tròn tâm I(1;2), bán kính r = 9

C. Đường tròn tâm I(1;-2), bán kính r = 3

D. Đường tròn tâm I(-1;2), bán kính r = 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 19

Cho hàm số $f (x) = l n \frac{2018 x}{x + 1} .$ Tính tổng $S = f' (1) + f' (2) + ... + f' (2018)$

A. $S = \frac{2018}{2019}$

B. S = 1

C. S = ln2018

D. S = 2018

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 20

Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh a, $S A ⊥ (A B C D)$ .Cạnh bên SC tạo với mặt đáy một góc 450. Tính thể tích V của khối chóp SABCD theo a.

A. $V = a^{3} \sqrt{2}$

B.

V = \frac{a^{3} \sqrt{3}}{3}

C.

V = \frac{a^{3} \sqrt{2}}{3}

D.

V = \frac{a^{3} \sqrt{2}}{6}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 21

Cho $\int_{0}^{3} \sqrt{9 - x^{2}} d x = \frac{a}{b} . π$ với $a, b \in ℤ$ và $\frac{a}{b}$ là phân số tối giản. Tính T = a.b

A. 35

B. 24

C. 12

D. 36

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 22

Trong mặt phẳng phức, cho điểm M trong hình vẽ bên là điểm biểu diễn số phức z. Trong các mệnh đề sau, mệnh đề nào SAI?

A. $z - \bar{z} = 6$

B. Số phức z có phần ảo là 4

C.

|z| = 5

D.

\bar{z} = 3 - 4 i

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 23

Trong không gian với hệ trục toạ độ Oxyz, cho hai đường thẳng $d_{1} : \{\begin{matrix} x = t \\ y = - 1 - 4 t \\ z = 6 + 6 t \end{matrix}$ và $d_{2} : \frac{x}{2} = \frac{y - 1}{1} = \frac{z + 2}{- 5}$ . Viết phương trình đường thẳng đi qua A(1;-1;2), đồng thời vuông góc với cả hai đường thẳng d1, d2?

A. $\frac{x - 1}{14} = \frac{y + 1}{17} = \frac{z - 2}{9}$

B.

\frac{x - 2}{2} = \frac{y + 1}{- 1} = \frac{z - 2}{4}

C.

\frac{x - 1}{3} = \frac{y + 1}{2} = \frac{z - 2}{4}

D.

\frac{x - 1}{1} = \frac{y + 1}{2} = \frac{z - 2}{3}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 24

Trong không gian với hệ trục toạ độ Oxyz, cho đường thẳng d là giao tuyến của hai mặt phẳng $(α) : x + y = 0, (α') : 2 x - y + z - 15 = 0;$ đường thẳng $d' : \{\begin{matrix} x = 1 - t \\ y = 2 + 2 t \\ z = 3 \end{matrix} .$ Tìm giao điểm của d và d’.

A. I(4;-4;3)

B. I(0;0;2)

C. I(1;2;3)

D. I(0;0;-1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 25

Cho hình chóp SABCD có đáy là hình thang vuông tại A và B. Hình chiếu vuông góc của S lên mặt đáy trùng với trung điểm của AB. Biết $A B = 1, B C = 2, B D = \sqrt{10} .$ Góc giữa (SBD) và mặt đáy là 60o. Tính thể tích của khối chóp SBCD

A. $\frac{\sqrt{30}}{4}$

B.

\frac{\sqrt{30}}{12}

C.

\frac{\sqrt{30}}{20}

D.

\frac{3 \sqrt{30}}{8}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 26

Trong không gian tọa độ Oxyz cho mặt phẳng $(P) : x - 2 y - z + 1 = 0.$ Vectơ nào dưới đây là một véc tơ pháp tuyến của mặt phẳng (P)?

A.

\vec{n} (1; 2; - 1)

B.

\vec{n} (1; - 2; - 1)

C.

\vec{n} (1; 0; 1)

D.

\vec{n} (1; - 2; 1)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 27

Cho hàm số $f (x) = \frac{3^{x - 2}}{7^{x^{2} - 4}} .$ Hỏi mệnh đề nào sau đây là mệnh đề sai?

A. $f (x) > 1 \Leftrightarrow (x - 2) \log 3 - (x^{2} - 4) \log 7 > 0$

B.

f (x) > 1 \Leftrightarrow (x - 2) \log_{0,3} 3 - (x^{2} - 4) \log_{0,3} 7 > 0

C.

f (x) > 1 \Leftrightarrow (x - 2) \ln 3 - (x^{2} - 4) \ln 7 > 0

D.

f (x) > 1 \Leftrightarrow x - 2 - (x^{2} - 4) \log_{3} 7 > 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 28

Gọi z1, z2 là hai nghiệm phức của phương trình $z^{2} + 3 z + 5 = 0$ . Tính $|z_{1} + z_{2}|$

A. 3

B.

\frac{3}{2}

C. 5

D.

\sqrt{3}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 29

Tìm hệ số của $x^{5}$ trong khai triển biểu thức ${(x^{2} + \frac{2}{x})}^{7}$

A.

8. C_{7}^{5}

B.

8. C_{7}^{3}

C.

C_{7}^{3}

D.

C_{7}^{2}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 30

Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng $(P) : x + 2 y - 2 z - 2 = 0,$ và điểm I(1;2;-3). Mặt cầu tâm I tiếp xúc với mặt phẳng (P) có bán kính là

A. $\frac{1}{3}$

B.

\frac{11}{3}

C. 1

D. 3

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 31

Trong không gian Oxyz, cho ba điểm $M (2; 0; 0), N (0; 1; 0), P (0; 0; 2) .$ Mặt phẳng (MNP) có phương trình là:

A. $\frac{x}{2} + \frac{y}{- 1} + \frac{z}{2} = 0$

B.

\frac{x}{2} + \frac{y}{- 1} + \frac{z}{2} = 1

C.

\frac{x}{2} + \frac{y}{1} + \frac{z}{2} = 1

D.

\frac{x}{2} + \frac{y}{- 1} + \frac{z}{2} = - 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 32

Tìm điểm cực tiểu của hàm số $y = - x^{3} + 3 x^{2} + 4.$

A. x = 2

B. M(0;4)

C. x = 0

D. M(2;0)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 33

Tìm tham số m để đồ thị hàm số $y = \frac{m x + 1}{x - m}$ đi qua A(1;-3).

A. m = -2

B. m = -1

C. m = 2

D. m = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 34

Cho hàm số y = f(x) có bảng biến thiên như hình vẽ sau:

Hàm số y = f(x) đồng biến trên khoảng nào trong các khoảng sau:

A. (0;3)

B.

(2; + \infty)

C.

(- \infty; 0)

D. (0;2)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 35

Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, BC=2a. Mặt bên (SAB)vuông góc với mặt đáy, biết ASB = 60 $°$ , SB = a. Gọi (S) là mặt cầu tâm B và tiếp xúc với mặt phẳng (SAC). Tính bán kính r của mặt cầu (S).

A. r = 2a

B.

r = 2 a \sqrt{\frac{3}{19}}

C.

r = 2 a \sqrt{3}

D.

r = a \sqrt{\frac{3}{19}}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 36

Cho hàm số y = f(x) có đạo hàm liên tục trên R và thỏa mãn $f (- 2) = 1; \int_{1}^{2} f (2 x - 4) d x = 1.$ Tính $I = \int_{- 2}^{0} x f' (x) d x .$

A. I = 1

B. I = 0

C. I = -4

D. I = 4

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 37

Tìm tập xác định của hàm số $y = {[x^{2} (x + 3)]}^{\sqrt{3}}$ .

A. $D = (- \infty; + \infty)$

B.

D = (- 3; + \infty) \ \{0\}

C.

D = (0; + \infty)

D.

D = (- 3; + \infty)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 38

Cho cấp số cộng (un) có các số hạng đều dương, số hạng đầu u1 = 1 và tổng của 100 số hạng đầu tiên bằng 14 950. Tính giá trị của tổng

$S = \frac{1}{u_{2} \sqrt{u_{1}} + u_{1} \sqrt{u_{2}}} + \frac{1}{u_{3} \sqrt{u_{2}} + u_{2} \sqrt{u_{3}}} + ... + \frac{1}{u_{2018} \sqrt{u_{2017}} + u_{2017} \sqrt{u_{2018}}}$

A.

\frac{1}{3} (1 - \frac{1}{\sqrt{6052}})

B.

1 - \frac{1}{\sqrt{6052}}

C. 2018

D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 39

Trong không gian với hệ trục tọa độOxyz, cho mặt cầu $(S_{1}) : {(x - 1)}^{2} + {(y - 1)}^{2} + {(z - 2)}^{2} = 16, (S_{2}) : {(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 1)}^{2} = 9$ cắt nhau theo giao tuyến là đường tròn (C). Tìm tọa độ tâm J của đường tròn (C).

A. $J (- \frac{1}{2}; \frac{7}{4}; \frac{1}{4})$

B.

J (\frac{1}{3}; \frac{7}{4}; \frac{1}{4})

C.

J (- \frac{1}{3}; \frac{7}{4}; - \frac{1}{4})

D.

J (- \frac{1}{2}; \frac{7}{4}; - \frac{1}{4})

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 40

Trong không gian Oxyz, cho các điểm $A (4; 2; 5); B (0; 4; - 3); C (2; - 3; 7) .$ Biết điểm $M (x_{0}; y_{0}; z_{0})$ nằm trên mặt phẳng (Oxy) sao cho $|\vec{M A} + \vec{M B} + \vec{M C}|$ đạt giá trị nhỏ nhất. Tính tổng $P = x_{0} + y_{0} + z_{0} .$

A. P = -3

B. P = 0

C. P = 3

D. P = 6

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 41

Biết đồ thị hàm số $y = (m - 4) x^{3} - 6 (m - 4) x^{2} - 12 m x + 7 m - 18$ (với m là tham số thực) có ba điểm cố định thẳng hàng. Viết phương trình đường thẳng đi qua ba điểm cố định đó.

A. $y = - 48 x + 10$

B.

y = \sqrt{3} x - 1

C.

y = x - 2

D.

y = 2 x - 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 42

Cho một tập hợp có 2018 phần tử. Hỏi tập đó có bao nhiêu tập con mà mỗi tập con đó có số phần tử là một số lẻ.

A. 1009

B.

2^{2018} - 1

C.

2^{2018}

D.

2^{2017}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 43

Số nghiệm thực của phương trình $2018^{x} + \frac{1}{1 - x} - \frac{1}{x - 2018} = 2018$ là

A. 3

B. 0

C. 2018

D. 1

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 44

Cho phương trình $z^{4} - 2 z^{3} + 6 z^{2} - 8 z + 9 = 0.$ Có 4 nghiệm phức phân biệt là $z_{1}, z_{2}, z_{3}, z_{4}$ .Tính giá trị biểu thức $T = (z_{1}^{2} + 4) (z_{2}^{2} + 4) (z_{3}^{2} + 4) (z_{4}^{2} + 4)$

A. T = 2i

B. T = 1

C. T = -2i

D. T = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 45

Từ các chữ số 1;2;3;4;5;6 lập được bao nhiêu số tự nhiên gồm 8 chữ số sao cho trong mỗi số đó có đúng ba chữ số 1, các chữ số còn lại đôi một khác nhau và hai chữ số chẵn không đứng cạnh nhau?

A. 2612

B. 2400

C. 1376

D. 2530

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 46

Cho hàm số $f (x) = x^{3} + m x^{2} + n x - 1$ với m,n là các tham số thực thỏa mãn $\{\begin{matrix} m + n > 0 \\ 7 + 2 (2 m + n) < 0 \end{matrix} .$ Tìm số điểm cực trị của hàm số $y = |f (|x|)| .$

A. 2

B. 9

C. 11

D. 5

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 47

Tính diện tích hình phẳng giới hạn bởi các đường $y = x^{2} - 2, y = - |x|$

A. $\frac{13}{3}$

B.

\frac{7}{3}

C. 3

D.

\frac{11}{3}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 48

Cho hàm số $y = {(x + a)}^{3} + {(x + b)}^{3} - x^{3}$ với a, b là các số thực. Khi hàm số đồng biến trên R, hãy tìm giá trị nhỏ nhất của biểu thức $A = 4 (a^{2} + b^{2}) - (a + b) - a b$

A. $M i n A = - 2$

B.

M i n A = - \frac{1}{16}

C.

M i n A = - \frac{1}{4}

D.

M i n A = 0

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 49

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng $Δ : \frac{x - 1}{2} = \frac{y}{1} = \frac{z + 2}{- 1}$ và hai điểm $A (0; - 1; 3), B (1; - 2; 1) .$ Tìm tọa độ điểm M thuộc đường thẳng $Δ$ sao cho $M A^{2} + 2 M B^{2}$ đạt giá trị nhỏ nhất.

A. M(5;2;-4)

B. M(-1;-1;-1)

C. M(1;0;-2)

D. M(3;1;-3)

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP

Câu 50

Cho tứ diện ABCD, trên các cạnh BC, BD, AC lần lượt lấy các điểm M, N, P sao cho $B C = 3 B M, B D = \frac{3}{2} B N, A C = 2 A P .$ Mặt phẳng (MNP) chia khối tứ diện ABCD thành hai phần có thể
tích là $V_{1}, V_{2}$ . Tính tỉ số $\frac{V_{1}}{V_{2}}$ .

A. $\frac{V_{1}}{V_{2}} = \frac{26}{13}$

B.

\frac{V_{1}}{V_{2}} = \frac{26}{19}

C.

\frac{V_{1}}{V_{2}} = \frac{3}{19}

D.

\frac{V_{1}}{V_{2}} = \frac{15}{19}

Lời giải

Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.

Nâng cấp VIP