Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2021-2022 sở GD&ĐT Quảng Bình có đáp án
66 người thi tuần này 4.6 68 lượt thi 5 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề thi thử vào lớp 10 trường THCS Văn Quán (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Phú Diễn (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 Toán trường THCS Lê Lợi (Hà Nội) năm 2025-2026 Tháng 12 có đáp án
Đề thi thử vào lớp 10 trường THCS Thịnh Quang (Hà Nội) năm 2025-2026 Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Bắc Kạn năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Lắk năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Long An năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
a)Ta có: \(P = \frac{{{{\left( {\sqrt x + 1} \right)}^2} - {{\left( {\sqrt x - 1} \right)}^2} - 8\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}:\frac{{\sqrt x - x - 3 - \left( {\sqrt x + 1} \right)}}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}\)
\( = \,\frac{{ - 4\sqrt x }}{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}} \cdot \frac{{\left( {\sqrt x - 1} \right)\left( {\sqrt x + 1} \right)}}{{ - x - 4}} = \frac{{4\sqrt x }}{{x + 4}}.\)
Vậy \(P = \frac{{4\sqrt x }}{{x + 4}}.\)
b)Vì \(x \ge 0,{\rm{ }}x \ne 1\) nên \(P = \frac{{4\sqrt x }}{{x + 4}} \ge 0.\)
Ta có: \(1 - P = 1 - \frac{{4\sqrt x }}{{x + 4}} = \frac{{x - 4\sqrt x + 4}}{{x + 4}} = \frac{{{{\left( {\sqrt x - 2} \right)}^2}}}{{x + 4}} \ge 0\) suy ra \(P \le 1.\)
Do đó \(0 \le P \le 1\) mà \(P \in Z\) nên \(P = 0\) hoặc \(P = 1.\)
Với \(P = 0\) thì \(x = 0\) (thỏa mãn).
Với \(P = 1\) thì \(\sqrt x - 2 = 0 \Leftrightarrow x = 4\) (thỏa mãn).
Vậy \(x = 0;\,\,x = 4\) thì \(P\) nhận giá trị nguyên.
Lời giải
a)Xét phương trình hoành độ giao điểm của \(\left( d \right)\) và \(\left( P \right):\)
\({x^2} = 2mx - m + 1 \Leftrightarrow {x^2} - 2mx + m - 1 = 0\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Ta thấy \(\Delta ' = {m^2} - m + 1 = {\left( {m - \frac{1}{2}} \right)^2} + \frac{3}{4} > 0\), với mọi \(m \in \mathbb{R}.\)
Suy ra phương trình \(\left( 1 \right)\) có hai nghiệm phân biệt với mọi \(m \in \mathbb{R}.\)
Do đó đường thẳng \(\left( d \right)\) cắt \(\left( P \right)\) tại hai điểm phân biệt với mọi \(m \in \mathbb{R}.\)
Ta có \({x_1},{x_2}\) là hai nghiệm của phương trình \(\left( 1 \right)\)
Áp dụng định lí Vi-ét ta được \(\left\{ \begin{array}{l}{x_1} + {x_2} = 2m\\{x_1} \cdot {x_2} = m - 1\end{array} \right.\)
Ta có \(\left| {{x_1} - {x_2}} \right| > \sqrt 3 \Leftrightarrow {\left( {{x_1} - {x_2}} \right)^2} > 3 \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 4{x_1}{x_2} - 3 > 0.\)
\( \Leftrightarrow 4{m^2} - 4m + 1 > 0 \Leftrightarrow {\left( {2m - 1} \right)^2} > 0 \Leftrightarrow m \ne \frac{1}{2}.\)
Vậy \(m \ne \frac{1}{2}\) thì \(\left( d \right)\) và \(\left( P \right)\) cắt nhau tại hai điểm phân biệt có hoành độ \({x_1};\,\,{x_2}\) thỏa mãn \(\left| {{x_1} - {x_2}} \right| > \sqrt 3 .\)
b)Điều kiện: \(x \ge - \frac{1}{5}.\)
Ta có: \(8\sqrt {5x + 1} + 6\sqrt {2x + 3} = 7x + 29.\)
\( \Leftrightarrow \left( {5x + 1 - 8\sqrt {5x + 1} + 16} \right) + \left( {2x + 3 - 6\sqrt {2x + 3} + 9} \right) = 0\)
\( \Leftrightarrow {\left( {\sqrt {5x + 1} - 4} \right)^2} + {\left( {\sqrt {2x + 3} - 3} \right)^2} = 0\)
\( \Leftrightarrow \left\{ \begin{array}{l}\sqrt {5x + 1} - 4 = 0\\\sqrt {2x + 3} - 3 = 0\end{array} \right. \Leftrightarrow x = 3\) (thỏa mãn).
Vậy phương trình có nghiệm \(x = 3.\)
Lời giải
Do \(x,{\rm{ }}y \in \left[ {5;7} \right] \Rightarrow \left| {x - y} \right| \le 2 \Leftrightarrow {\left( {x - y} \right)^2} \le 4\)
\( \Leftrightarrow {x^2} - 2xy + {y^2} \le 4 \Leftrightarrow {\left( {x + y} \right)^2} \le 4\left( {xy + 1} \right) \Leftrightarrow x + y \le 2\sqrt {xy + 1} \)
Chứng minh tương tự ta có:
\(y + z \le 2\sqrt {yz + 1} ;\)\(z + x \le 2\sqrt {zx + 1} \)
Cộng vế theo vế các bất đẳng thức trên, ta có
\[2\left( {x + y + z} \right) \le 2\left( {\sqrt {xy + 1} + \sqrt {yz + 1} + \sqrt {zx} } \right)\]
\( \Leftrightarrow \sqrt {xy + 1} + \sqrt {yz + 1} + \sqrt {zx + 1} \ge x + y + z\)
Dấu bằng xảy ra khi \(\left\{ \begin{array}{l}\left| {x - y} \right| = 2\,\,\,\,\,\,\,\\\left| {y - z} \right| = 2\,\,\,\,\,\,\\\left| {z - x} \right| = 2\,\,\,\,\,\,\end{array} \right.\left( 1 \right)\)
Vì \(x \ne y \ne z\) nên giả sử \(x > y > z.\)
Ta có \(\left( 1 \right) \Leftrightarrow \left\{ \begin{array}{l}x - y = 2\\y - z = 2\\x - z = 2\end{array} \right.\,\,\, \Leftrightarrow \left\{ \begin{array}{l}x - y = 2\\x - z = 4\\x - z = 2\end{array} \right.\) (vô nghiệm)
Vậy \(\sqrt {xy + 1} + \sqrt {yz + 1} + \sqrt {zx + 1} > x + y + z.\)
Lời giải
Đặt \({n^2} - 2n - 7 = {a^3};\,\,{n^2} - 2n + 12 = {b^3}\) (với \(a,{\rm{ }}b \in {\mathbb{N}^*}\))
Dễ thấy \(a < b\)
Ta có \({b^3} - {a^3} = \left( {{n^2} - 2n + 12} \right) - \left( {{n^2} - 2n - 7} \right) = 19\)
\( \Leftrightarrow \left( {b - a} \right)\left( {{b^2} + ab + {a^2}} \right) = 19\)
Vì \(a,{\rm{ }}b \in {\mathbb{N}^*}\), \(b > a\), \({b^2} + ab + {a^2} > b - a\) và \(19\) là số nguyên tố nên
\(\left\{ \begin{array}{l}b - a = 1\\{b^2} + ab + {a^2} = 19\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\left( {TM} \right)\\\left\{ \begin{array}{l}a = - 3\\b = - 2\end{array} \right.\left( L \right)\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\)
\( \Rightarrow {n^2} - 2n - 15 = 0 \Leftrightarrow \left[ \begin{array}{l}n = - 3{\rm{ }}(L)\\n = 5{\rm{ }}(TM)\end{array} \right. \Leftrightarrow n = 5\)
Vậy \(n = 5\) là giá trị cần tìm.
Lời giải
Hình vẽ
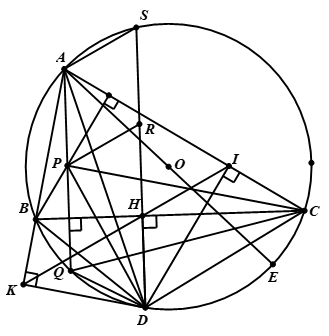
a)Tứ giác \(BKDH\) nội tiếp \[ \Rightarrow \widehat {KBD} = \widehat {KHD}{\rm{ }}\left( 1 \right).\]
Tứ giác \(ABDC\) nội tiếp \( \Rightarrow \widehat {KBD} = \widehat {ACD}{\rm{ }}\left( 2 \right)\) (cùng bù với \(\widehat {ABD}\))
Từ \(\left( 1 \right),\left( 2 \right) \Rightarrow \widehat {KHD} = \widehat {ICD}{\rm{ }}\left( 3 \right).\)
Lại có tứ giác \(CIHD\) nội tiếp \( \Rightarrow \widehat {IHD} + \widehat {ICD} = {180^0}{\rm{ }}\left( 4 \right).\)
Từ \(\left( 3 \right),{\kern 1pt} \;\left( 4 \right)\) suy ra \(\widehat {IHD} + \widehat {DHK} = {180^0}\)
\( \Rightarrow K,\,I,\,H\) thẳng hàng.
\( \Rightarrow \frac{{CH}}{{HD}} = \frac{{AB}}{{KD}} + \frac{{BK}}{{KD}}\,\,\,\,\,\,\left( 5 \right)\)
b)\( \Rightarrow \frac{{BH}}{{DH}} = \frac{{AC}}{{DI}} - \frac{{IC}}{{DI}}\,\,\,\,\,\,\,\left( 6 \right)\)
Từ \(\left( 5 \right),{\rm{ }}\left( 6 \right)\) và \(\left( 7 \right)\) suy ra \(\frac{{CH}}{{HD}} + \frac{{BH}}{{DH}} = \frac{{AB}}{{KD}} + \frac{{AC}}{{DI}}.\)
Vậy \(\frac{{AC}}{{DI}} + \frac{{AB}}{{DK}} = \frac{{BC}}{{DH}} \cdot \)
c)Đường thẳng \(AP\) cắt \(\left( O \right)\) tại \(Q\) và đường thẳng \(DH\) cắt \(\left( O \right)\) tại \(S.\)
Ta có \(\widehat {SAC} = \widehat {SDC}\) (cùng chắn )
Tứ giác \(CDHI\) nội tiếp \( \Rightarrow \widehat {HDC} = \widehat {HIA} \Rightarrow \widehat {SAC} = \widehat {HIA}\)
Suy ra đường thẳng \[AS\] song song với đường thẳng \[HK.\]
Ta có \(AQ\)//\(DS\) (cùng vuông góc với \(BC\))
\( \Rightarrow AQDS\) là hình thang, nội tiếp đường tròn \(\left( O \right)\)
\( \Rightarrow AQDS\) là hình thang cân \( \Rightarrow \widehat {QDS} = \widehat {ASD}.\)
Qua \(P\) vẽ \[PR\]//\[AS \Rightarrow \widehat {ASD} = \widehat {PRD}\] (đồng vị)
Suy ra \(\widehat {PRD} = \widehat {QDR} \Rightarrow PQDR\) là hình thang cân
Ta thấy \(BC \bot PQ\) tại trung điểm \(PQ\), suy ra \(BC\) là trục đối xứng của hình thang cân \( \Rightarrow HD = HR.\)
Xét \(\Delta DPR\) có \(HD = HR\) và \[HK\]//\[PR\]
\( \Rightarrow HK\) đi qua trung điểm của \(DP.\)