Đề thi tuyển sinh vào lớp 10 môn Toán năm 2023-2024 Chuyên Hòa Bình có đáp án

1)\(A = (\sqrt 5 - 1)\sqrt {{{(\sqrt 5 + 1)}^2}} \)

\(A = (\sqrt 5 - 1)(\sqrt 5 + 1) = 4\)

2)Theo ĐL Viét, ta có: \(\left\{ \begin{array}{l}{x_1} + {x_2} = 1\\{x_1}{x_2} = - 3\end{array} \right.\)

\[B = \frac{{{x_1}}}{{{x_2}}} + \frac{{{x_2}}}{{{x_1}}} = \frac{{{x_1}^2 + {x_2}^2}}{{{x_1}{x_2}}} = \frac{{{{({x_1} + {x_2})}^2} - 2{x_1}{x_2}}}{{{x_1}{x_2}}} = \frac{{{1^2} - 2.( - 3)}}{{ - 3}} = \frac{{ - 7}}{3}\]           

3)ĐK: \(m \ne - 2\)

\( \oplus \,\,A(\frac{{ - 3}}{{m + 2}};0) \Rightarrow OA = \left| {\frac{{ - 3}}{{m + 2}}} \right| = \frac{3}{{\left| {m + 2} \right|}}\)

\( \oplus \,\,B(0;3) \Rightarrow OB = 3\)

Ta có tam giác \(AOB\) cân tại \(O\) nên \(OA = OB\) \( \Leftrightarrow \left| {\frac{3}{{m + 2}}} \right| = 3\)

\( \Leftrightarrow \left[ \begin{array}{l}\frac{3}{{m + 2}} = 3\\\frac{3}{{m + 2}} = - 3\end{array} \right. \Rightarrow \left[ \begin{array}{l}m = - 1\,\,(TM)\\m = \,\, - 3\,\,(TM)\end{array} \right.\)

1)\((4{x^2} - 7x + 4)(3{x^2} - 4x + 3) = 3{x^2}\)   (1)

Ta thấy x = 0 không phải là nghiệm của phương trình (1).

Xét x khác 0, chia cả 2 vế của (1) cho \({x^2}\) ta được phương trình.

\(\left( {4x - 7 + \frac{4}{x}} \right)\left( {3x - 4 + \frac{3}{x}} \right) = 3 \Leftrightarrow \left[ {4\left( {x + \frac{1}{x}} \right) - 7} \right].\left[ {3\left( {x + \frac{1}{x}} \right) - 4} \right] = 3\)

Đặt \(x + \frac{1}{x} = t\). Ta được phương trình:

\((4t - 7)(3t - 4) = 3 \Leftrightarrow 12{t^2} - 37t + 25 = 0 \Leftrightarrow \left[ \begin{array}{l}t = 1\\t = \frac{{25}}{{12}}\end{array} \right.\)

* Với t = 1\( \Rightarrow x + \frac{1}{x} = 1 \Leftrightarrow {x^2} - x + 1 = 0\) (Phương trình vô nghiệm).

* Với t = \(\frac{{25}}{{12}}\)\( \Rightarrow x + \frac{1}{x} = \frac{{25}}{{12}} \Rightarrow 12{x^2} - 25x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{4}{3}\\x = \frac{3}{4}\end{array} \right.\). KL....

2)\(\left\{ \begin{array}{l}x + my = 3m - 3\\mx + y = 2m - 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + my = 3m - 3\\({m^2} - 1)x = 2{m^2} - 5m + 3\end{array} \right.\)

Để hệ phương trình có nghiệm duy nhất thì \({m^2} - 1 \ne 0 \Leftrightarrow m \ne \pm 1\)

Suy ra hệ phương trình có nghiệm duy nhất là\(\left\{ \begin{array}{l}x = \frac{{2m - 3}}{{m + 1}} = 2 - \frac{5}{{m + 1}}\\y = 3 - \frac{5}{{m + 1}}\end{array} \right.\)

Vì m nguyên để hệ phương trình có nghiệm duy nhất là các số nguyên thì m + 1 phải là ước của 5\( \Rightarrow m + 1 \in \left\{ {1; - 1;5; - 5} \right\}\)

\( \Rightarrow m \in \left\{ {0; - 2;4; - 6} \right\}(TM)\). KL...

3)Gọi số lần đi của Robot (theo quy luật đi rồi lại nghỉ) là x (x > 1, x\( \in {{\rm N}^*}\))

Thời gian đi của Robot theo quy luật là: \(\frac{{120}}{{40}} + \frac{{240}}{{40}} + \frac{{360}}{{40}} + ... + \frac{{120x}}{{40}} = 3 + 6 + 9 + ... + 3x = \frac{{3x(x + 1)}}{2}\) (phút)

Thời gian nghỉ của Robot là: \(1 + 2 + 3 + .... + x - 1 = \frac{{x(x - 1)}}{2}\) (phút)

Theo bài ra ta có phương trình: \(\frac{{3x(x + 1)}}{2} + \frac{{x(x - 1)}}{2} = 253 \Leftrightarrow 2{x^2} + x - 253 = 0\)

Giải phương trình tìm được: \({x_1} = 11\,\,(TM);\,\,{x_2} = - \frac{{23}}{2}\,\,(KTM)\)

Quãng đường từ A đến B là: \(\frac{{3.11.12}}{2}.40 = 7920\,\,(cm)\)

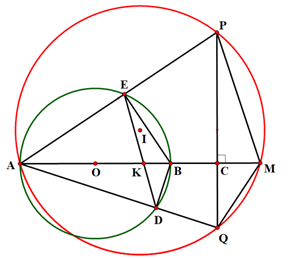
a)\[\widehat {BEP} + \widehat {BCP} = {90^0} + {90^0} = {180^0}\] ½ tứ giác \[BEPC\] nội tiếp.

\[ \Rightarrow \widehat {EPC} = \widehat {EBA}\] (vì cùng bù với \[\widehat {EBC}\])

\[ \Rightarrow \widehat {EDA} = \widehat {EBA}\] (góc nội tiếp cùng chắn cung AE)

\[ \Rightarrow \widehat {EDA} = \widehat {APQ} \Rightarrow \] Tứ giác \(PEDQ\) nội tiếp.

b)Mà \[\widehat {AMQ} = \widehat {APQ} \Rightarrow \widehat {APQ} = \widehat {ADE}\] \[ \Rightarrow \widehat {AMQ} = \widehat {ADK}\]

\[ \Rightarrow \Delta AKD\, \sim \,\Delta AQM{\rm{ }}\,\,(\widehat {QAM}\,\,chung;\,\,\widehat {ADK} = \widehat {AMQ})\]

c)\( \Rightarrow \Delta AKD\, \sim \,\Delta AQM{\rm{ }} \Rightarrow \frac{{AK}}{{AQ}} = \frac{{AD}}{{AM}} \Rightarrow AK.AM = AD.AQ\)

Ta có: \(\Delta ADB\,\, \sim \Delta ACQ\,{\rm{ }}(\widehat A{\rm{ chung;}}\,\,\widehat {ADB} = \widehat {ACQ} = {90^0})\)

\( \Rightarrow \frac{{AD}}{{AC}} = \frac{{AB}}{{AQ}} \Rightarrow AB.AC = AD.AQ\) \( \Rightarrow AK.AM = AB.AC\)

d)Ta có \(AK.AM = AB.AC \Rightarrow AM = \frac{{AB.AC}}{{AK}}\)(không đổi) ½ \(M\) cố định.

Gọi I là tâm đường tròn ngoại tiếp tam giác \(APQ\) thì ta có \(IA = IM\) nên \(I\) nằm trên đường trung trực của \(AM\) cố định.

1)ĐKXĐ: \(x \le 1;y \ge 1\)

\((1) \Leftrightarrow (1 - x)\sqrt {1 - x} - (y - 1)\sqrt {y - 1} + \sqrt {1 - x} - \sqrt {y - 1} = 0\)

Đặt \(\sqrt {1 - x} = u\,\,(u \ge 0);\,\,\sqrt {y - 1} = t\,\,(t \ge 0)\) ta được phương trình:

\({u^3} - {t^3} + u - t = 0\)\( \Leftrightarrow (u - t)({u^2} + ut + {t^2} + 1) = 0 \Leftrightarrow \left[ \begin{array}{l}u - t = 0\\{u^2} + ut + {t^2} + 1 = 0\end{array} \right.\)

\( \Leftrightarrow \,\,\,u - t = 0 \Rightarrow 1 - x = y - 1 \Leftrightarrow x = 2 - y\).

Từ (2) suy ra \(\sqrt {4 - y} + \sqrt {y + 1} = 3\) (ĐKXĐ: \(1 \le y \le 4\))

\(\begin{array}{l} \Rightarrow 5 + 2\sqrt {(4 - y)(y + 1)} = 9 \Leftrightarrow \sqrt {4 + 3y - {y^2}} = 2 \Rightarrow 3y - {y^2} = 0\\ \Leftrightarrow \left[ \begin{array}{l}y = 0\,\,\,(KTM)\\y = 3\,\,\,(TM)\end{array} \right.\end{array}\)

Vậy hệ có nghiệm \((x;y) = ( - 1;3).\)

2)Từ giả thiết \[{\rm{a}}\left( {a - 1} \right) + b\left( {b - 1} \right) = ab \Rightarrow {a^2} + {b^2} - \left( {a + b} \right) = ab\]

\[ \Rightarrow {a^2} + {b^2} = ab + a + b\]

Theo bất đẳng thức AM-GM, ta có: \[{a^2} + {b^2} \ge 2{\rm{a}}b \Rightarrow ab + a + b \ge 2{\rm{a}}b \Rightarrow a + b \ge ab\,\,\,\,\,(1)\]

Lại có: \[{\rm{a}}b + a + b + 8 = \left( {{a^2} + 4} \right) + \left( {{b^2} + 4} \right) \ge 4{\rm{a}} + 4b = 4\left( {a + b} \right)\]

\[ \Rightarrow ab + 8 \ge 3\left( {a + b} \right) \ge 3ab\,\,(do\,\,\,(1))\]

\( \Rightarrow ab \le 4\).

Đặt \(t = \sqrt {ab} \Rightarrow 0 < t \le 2 \Rightarrow \frac{2}{t} \ge 1 \Rightarrow \frac{4}{{{t^2}}} \ge 1\).

Áp dụng bất đẳng thức AM-GM, ta có:

\[\begin{array}{l}F = \frac{{{a^2}}}{b} + \frac{{{b^2}}}{a} + 2023\left( {\frac{1}{a} + \frac{1}{b}} \right) + \frac{4}{{ab}} \ge 2\sqrt {\frac{{{a^2}}}{b}.\frac{{{b^2}}}{a}} + 2023.2\sqrt {\frac{1}{{ab}}} + \frac{4}{{ab}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2t + 4046.\frac{1}{t} + \frac{4}{{{t^2}}}\end{array}\]

\(F \ge 2t + \frac{8}{t} + 2019 \cdot \frac{2}{t} + \frac{4}{{{t^2}}}\).

Theo bất đẳng thức AM-GM, ta có \(2t + \frac{8}{t} \ge 2\sqrt {2t.\frac{8}{t}} = 8\)

\( \Rightarrow F \ge 8 + 2019 + 1 = 2028\). Vậy \(\min F = 2028\), đạt khi \(a = b = 2\).