Đề KSCL THCS Văn Quán - HN_năm học 2025-2026_Tháng 12 có đáp án
194 người thi tuần này 4.6 194 lượt thi 6 câu hỏi 45 phút
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
🔥 Học sinh cũng đã học
Đề KSCL THCS Văn Quán - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Phú Diễn - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Lê Lợi - HN_năm học 2025-2026_Tháng 12 có đáp án
Đề KSCL THCS Thịnh Quang - HN_năm học 2025-2026_Tháng 9 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Nông năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Bắc Kạn năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Đắk Lắk năm học 2025-2026 có đáp án
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Long An năm học 2025-2026 có đáp án
Danh sách câu hỏi:
Lời giải
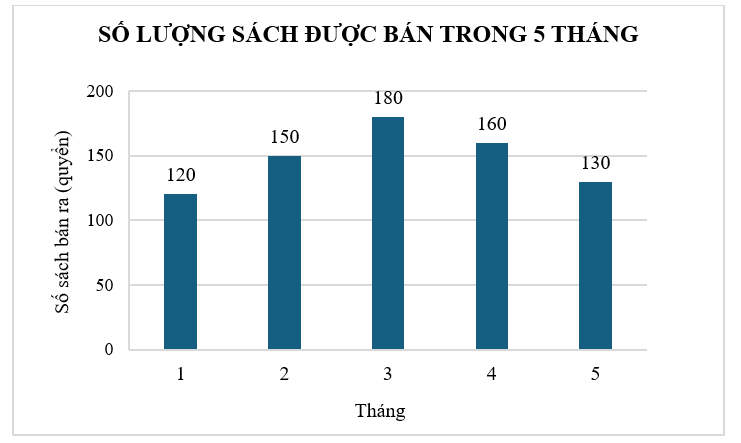
a) Quan sát vào biểu đồ trên, ta thấy:
− Tháng 3 nhà sách bán được nhiều sách tham khảo nhất (180 quyển);
− Tháng 1 nhà sách bán được ít sách tham khảo nhất (120 quyển).
b) Tổng số sách bán được trong 5 tháng là: \(120 + 150 + 180 + 160 + 130 = 740\) (quyển).
Số sách bán được trong tháng 2 là 150 quyển.
Tỉ lệ phần trăm số sách tham khảo cửa hàng bán được trong tháng 2 là:
\(\frac{{150}}{{740}} \cdot 100\% \approx 20,27\% .\)
Vậy tỉ lệ phần trăm số sách bán được tỏng tháng 2 khoảng \(20,27\% .\)
2) Tổng số tấm thẻ là 20 nên số kết quả có thể xảy ra khi lấy ngẫu nhiên một tấm thẻ là 20.
Các số chia hết cho 5 trong khoảng từ 1 đến 20 là \(5\,;\,\,10\,;\,\,15\,;\,\,20.\)
Suy ra có 4 kết quả thuận lợi cho biến cố “Lấy được thẻ có số chia hết cho 5”.
Xác suất của biến cố “Lấy được thẻ có số chia hết cho 5” là: \(P = \frac{4}{{20}} = \frac{1}{5}.\)
Lời giải
1)
a) \(7 + 2\sqrt 3 - \sqrt {48} + \sqrt {{{\left( {2 - \sqrt 3 } \right)}^2}} = 7 + 2\sqrt 3 - 4\sqrt 3 + 2 - \sqrt 3 = 9 - 3\sqrt 3 \)
b) \(\sqrt {45} - 10\sqrt {\frac{4}{5}} + \frac{{\sqrt 5 - 5}}{{\sqrt 5 }} = 3\sqrt 5 - 4\sqrt 5 + 1 - \sqrt 5 = 1 - 2\sqrt 5 \)
2)
a) \(\sqrt {{x^2} - 4x + 4} = 7\) (ĐKXĐ: \(x \in R\))
\(\sqrt {{{\left( {x - 2} \right)}^2}} = 7\)
\(\left| {x - 2} \right| = 7\)
\(x - 2 = 7\) hoặc \(x - 2 = - 7\)
\(x = 9\,\,{\rm{(TM)}}\) hoặc \(x = - 5\,\,{\rm{(TM)}}\)
Vậy phương trình có nghiệm là \(x \in \left\{ {9; - 5} \right\}\)
b) \(5\sqrt[3]{{x - 2}} + \sqrt[3]{{8{\rm{x}} - 16}} - \sqrt[3]{{27x - 54}} + 4 = 0\)
\(5\sqrt[3]{{x - 2}} + 2\sqrt[3]{{x - 2}} - 3\sqrt[3]{{x - 2}} + 4 = 0\)
\(4\sqrt[3]{{x - 2}} = - 4\)
\(\begin{array}{l}\sqrt[3]{{x - 2}} = - 1\\x - 2 = - 1\\x = 1\end{array}\)
Vậy phương trình có nghiệm là x = 1.
Lời giải
1) Gọi vận tốc ô tô là x (km/h), x > 20
Vận tốc xe máy là x – 20 (km/h)
Thời gian đi của ô tô là: \(\frac{{120}}{x}\) (h)
Thời gian đi của xe máy là: \(\frac{{120}}{{x - 20}}\) (h)
Vì xe máy đến B muộn hơn xe ô tô là 1 giờ nên ta có phương trình: \(\frac{{120}}{{x - 20}} - \frac{{120}}{x} = 1\)
Hay: \({x^2} - 20x - 2400 = 0\)
Nên \(\left( {x - 60} \right)\left( {x + 40} \right) = 0\)
Ta được \(x = 60(TM);\,x = - 40(KTM)\)
Vậy vận tốc của ô tô là 60km/h; vận tốc của xe máy là 40km/h
2) Gọi số tiền tiết kiệm mà chị Ngân gửi là x (đồng), x > 0
Tiền lãi chị Ngân nhận được sau 12 tháng là: \(6,2\% x\)( đồng)
Tổng số tiền chị Ngân nhận được sau khi gửi 12 tháng là \(x + 6,2\% x = 106,2\% x\)(đồng)
Chị Ngân dự định tổng số tiền nhận được sau khi gửi 12 tháng ít nhất là 318 600 000 đồng nên ta có bất phương trình:
\(106,2\% x \ge 318600000\)
\(x \ge 300000000\)
Vì x nhỏ nhất nên \(x = 300000000\)
Vậy chị Ngân phải gửi số tiền tiết kiệm ít nhất là 300 000 000 đồng.
Lời giải
Hình vẽ minh họa bài toán.
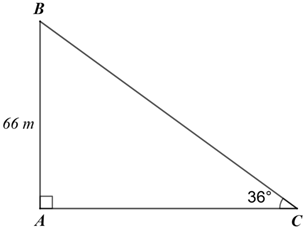
Độ cao của ngọn hải đăng là \(AB = 66\,\,{\rm{m}}\,{\rm{;}}\)
Góc giữa thuyền và tia nắng chiều từ đỉnh ngọn hải đăng đến thuyền là \(\widehat C = 36^\circ .\)
Xét \[\Delta ABC\] vuông tại \[A,\] ta có: \(\tan C = \frac{{AB}}{{AC}}\) (tỉ số lượng giác của góc nhọn).
Suy ra \(AC = \frac{{AB}}{{\tan C}} = \frac{{66}}{{\tan 36^\circ }} \approx 90,84\,\,({\rm{m}}).\)
Vậy khoảng cách của thuyền đến ngọn hải đăng khoảng \(90,84\,\,{\rm{m}}\,.\)
Lời giải
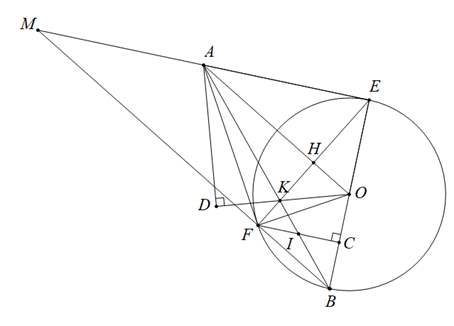
a) Vì \[AD \bot DO\] (gt) nên \[\widehat {ADO} = 90^\circ \], khi đó \[\Delta ADO\] vuông tại \[D\]
Vì \[\Delta ADO\] vuông tại \[D\] nên ba điểm \[A,D,O\] cùng thuộc đường tròn đường kính \[AO\] (1)
Vì \[AE\] là tiếp tuyến của \[\left( O \right)\] nên \[AE \bot OE\], do đó \[\widehat {AEO} = 90^\circ \], khi đó \[\Delta AEO\] vuông tại \[E\]
Vì \[\Delta AEO\] vuông tại \[E\] nên ba điểm \[A,E,O\] cùng thuộc đường tròn đường kính \[AO\] (2)
Từ (1), (2) suy ra bốn điểm \(D,A,E,O\) cùng thuộc một đường tròn.
b) Xét \[\Delta AEO\] và \[\Delta AFO\] có:
\[EO = FO\left( { = R} \right)\]
\[\widehat {EOA} = \widehat {FOA}\] (gt)
\[AO\] chung
Do đó \[\Delta AEO = \Delta AFO\] (c.g.c)
Suy ra \[\widehat {AFO} = \widehat {AEO}\] (hai góc tương ứng)
Mà \[\widehat {AEO} = 90^\circ \] nên \[\widehat {AFO} = 90^\circ \]
Xét \[\left( O \right)\] có \[AF \bot FO\] tại \[F \in \left( O \right)\] nên \[AF\] là tiếp tuyến của \[\left( O \right)\] tại tiếp điểm \(F\).
Vì \[OE = OF\] nên \[O\] thuộc đường trung trực của \[FE\]
Vì \[AF = AE\]nên \[A\] thuộc đường trung trực của \[FE\]
Do đó \[AO\] là đường trung trực \[FE\].
Suy ra \[AO \bot FE\] tại \[H\]
Xét \[\Delta OHK\] và \[\Delta ODA\] có:
\[\widehat {AOD}\] chung
\[\widehat {OHK} = \widehat {ODA} = 90^\circ \]
Do đó (g.g)
Suy ra \[\frac{{OK}}{{OA}} = \frac{{OH}}{{OD}}\], khi đó \[OK.OD = OH.OA\]
c) Gọi \(M\) là giao điểm của \(BF;AE\).
\(\Delta BFE\) có \(OB = OE = FO = \frac{{BE}}{2}\) nên \(\Delta BFE\) vuông tại \(F\).
Suy ra \(BM \bot FE\) mà \[AO \bot FE\] nên \(AO\,{\rm{//}}\,BM\)
\(\Delta BEM\) có \(AO\,{\rm{//}}\,BM\) và \(O\) là trung điểm của \(BE\) nên \(A\) là trung điểm của \(EM\) hay \(AM = AE\)
Có \(AE \bot BE;FC \bot BE \Rightarrow AE\,{\rm{//}}\,FC\)
Vì \(AE\,{\rm{//}}\,FC\) nên theo định lí Thalès ta có: \(\frac{{IC}}{{AE}} = \frac{{BI}}{{BA}}\) và \[\frac{{FI}}{{AM}} = \frac{{BI}}{{BA}}\]
Nên \(\frac{{IC}}{{AE}} = \frac{{FI}}{{AM}}\) mà \(AM = AE\) nên \(IC = FI\) hay \[I\] là trung điểm của \[FC\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.