Đề KSCL THCS Thịnh Quang - HN_năm học 2025-2026_Tháng 9 có đáp án

1) \(A = \sqrt 8  + 2\sqrt {18}  - 3\sqrt {32} \)\( = 2\sqrt 2  + 2.3\sqrt 2  - 3.4\sqrt 2 \)\( = 2\sqrt 2  + 6\sqrt 2  - 12\sqrt 2 \)\( =  - 4\sqrt 2 \)                    

2) \(B = \frac{2}{{\sqrt 3  - 1}} + \sqrt {{{\left( {1 - \sqrt 3 } \right)}^2}}  - \frac{{3\sqrt 6 }}{{\sqrt 2 }}\)\( = \frac{2}{{\sqrt 3  - 1}} + \sqrt 3  - 1 - 3\sqrt 3 \)\( = \frac{2}{{\sqrt 3  - 1}} - 1 - 2\sqrt 3 \)

\( = \frac{{2\left( {\sqrt 3  + 1} \right)}}{{\left( {\sqrt 3  - 1} \right)\left( {\sqrt 3  + 1} \right)}} - 1 - 2\sqrt 3 \)\( = \sqrt 3  + 1 - 1 - 2\sqrt 3 \)\( =  - \sqrt 3 \)

1) Khi \(x = 9\left( {tm} \right)\) giá trị biểu thức \(A\) là :

       \(A = \frac{{2.\sqrt 9  - 3}}{{\sqrt 9  - 1}}\)\( = \frac{{6 - 3}}{{3 - 1}}\)\( = \frac{3}{2}\)

Vậy \(A = \frac{3}{2}\)khi \(x = 9\)

2) \(B = \frac{{\sqrt x }}{{\sqrt x  - 1}} + \frac{5}{{\sqrt x  + 1}} - \frac{{8\sqrt x  - 6}}{{x - 1}}\)\( = \frac{{\sqrt x \left( {\sqrt x  + 1} \right)}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}} + \frac{{5\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} - \frac{{8\sqrt x  - 6}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\)

\( = \frac{{x + \sqrt x  + 5\sqrt x  - 5 - 8\sqrt x  + 6}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\)\( = \frac{{x - 2\sqrt x  + 1}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\)\( = \frac{{{{\left( {\sqrt x  - 1} \right)}^2}}}{{\left( {\sqrt x  - 1} \right)\left( {\sqrt x  + 1} \right)}}\)\[ = \frac{{\sqrt x  - 1}}{{\sqrt x  + 1}}\]

3) \(P = A.B\)\( = \frac{{2\sqrt x  - 3}}{{\sqrt x  - 1}}.\frac{{\sqrt x  - 1}}{{\sqrt x  + 1}}\)\( = \frac{{2\sqrt x  - 3}}{{\sqrt x  + 1}}\)\( = \frac{{2\left( {\sqrt x  + 1} \right) - 5}}{{\sqrt x  + 1}}\)\( = 2 - \frac{5}{{\sqrt x  + 1}}\)

+) Với \(x \ge 0\) ta có \(\sqrt x  + 1 > 0\)\( \Rightarrow \frac{{ - 5}}{{\sqrt x  + 1}} < 0\)\( \Rightarrow 2 - \frac{5}{{\sqrt x  + 1}} < 2\)\( \Rightarrow P < 2\) (1)

+) Với \(x \ge 0\) ta có \(\sqrt x  + 1 \ge 1\)\( \Rightarrow \frac{{ - 5}}{{\sqrt x  + 1}} \ge  - 5\)\( \Rightarrow 2 - \frac{5}{{\sqrt x  + 1}} \ge  - 3\)\( \Rightarrow P \ge  - 3\) (2)

Từ (1) và (2) ta có \( \Rightarrow  - 3 \le P < 2\), mà \(P \in \mathbb{Z}\), \(P\,m{\rm{ax}}\) nên \(P\, = 1\)

       \(2 - \frac{5}{{\sqrt x  + 1}} = 1\)\( \Rightarrow \frac{5}{{\sqrt x  + 1}} = 1\)\( \Rightarrow \sqrt x  + 1 = 5\)\( \Rightarrow x = 16\left( {tm} \right)\)

Vậy \(x = 16\)là giá trị cần tìm.

1) Giải phương trình sau :

a)   \(3\sqrt {x - 2}  - 5 = 4\)   Đk : \(x \ge 2\)

\(3\sqrt {x - 2}  = 9\)

\(\sqrt {x - 2}  = 3\)

\(x - 2 = 9\)

\(x = 11\left( {tm} \right)\)

Vậy \(x = 11\) là nghiệm của phương trình.

b)       \(\sqrt {4x - 20}  + 4\sqrt {x - 5}  = 8 + 16\sqrt {\frac{{x - 5}}{{64}}} \)  ĐK. \(x \ge 5\)

\(2\sqrt {x - 5}  + 4\sqrt {x - 5}  - 16.\frac{1}{8}\sqrt {x - 5}  = 8\)

\(4\sqrt {x - 5}  = 8\)

\(\sqrt {x - 5}  = 2\)

\(x = 9\left( {tm} \right)\)

Vậy \(x = 9\) là nghiệm của phương trình.

2) +) Có \(20\)kết quả

  Xét biến cố : “Số xuất hiện trên viên bi được lấy ta chia 7 dư 1”\[\]

+) Có \(3\)kết quả thuận lợi cho biến cố là \(1;8;15\)

+) Xác suất của biến cố là \(\frac{3}{{20}}\)

1) Gọi \(x,y\) (ngày) lần lượt là thời gian người thứ nhất và người thứ hai làm một mình xong công việc (\(x,y > 6\)). Khi đó:

Trong một ngày người thứ nhất làm được \(\frac{1}{x}\) (công việc).

Trong một ngày người thứ hai làm được \(\frac{1}{y}\) (công việc).

Trong một ngày cả hai người làm được \(\frac{1}{6}\) (công việc)  nên ta có phương trình: \(\frac{1}{x} + \frac{1}{y} = \frac{1}{6}\).   (1)

Nếu người thứ nhất làm \(3\)ngày, người thứ hai làm \(7\)ngày thì họ làm xong việc nên ta có phương trình: \(\frac{3}{x} + \frac{7}{y} = 1\).    (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}\frac{1}{x} + \frac{1}{y} = \frac{1}{6}\\\frac{3}{x} + \frac{7}{y} = 1\end{array} \right.\).

Đặt , \(b = \frac{1}{y}\), ta được: \(\left\{ \begin{array}{l}a + b = \frac{1}{6}\\3a + 7b = 1\end{array} \right.\,\,\,\,\,\,\,\,\,\,\)

\(\left\{ \begin{array}{l}7a + 7b = \frac{7}{6}\\3a + 7b = 1\end{array} \right.\,\,\,\,\,\,\,\,\,\,\)

\(\left\{ \begin{array}{l}4a = \frac{1}{6}\\a + b = \frac{1}{6}\end{array} \right.\,\,\,\,\,\,\,\,\,\,\)

\(\,\left\{ \begin{array}{l}a = \frac{1}{{24}}\\b = \frac{1}{{48}}\end{array} \right.\,\,\,\,\,\,\,\,\,\,\)

Mà \(a = \frac{1}{x}\), \(b = \frac{1}{y}\) nên:\(\,\,\left\{ \begin{array}{l}\frac{1}{x} = \frac{1}{{24}}\\\frac{1}{y} = \frac{1}{{48}}\end{array} \right.\,\,\,\,\,\,\,\,\)           \(\,\,\,\left\{ \begin{array}{l}x = 24\\y = 48\end{array} \right.\) (thỏa mãn).

Vậy nếu làm một mình thì người thứ nhất hoàn thành công việc trong \(24\) ngày, người thứ hai hoàn thành công việc trong \(48\)ngày.

2) Gọi số câu trả lời đúng của bạn Mai là \(x\) (câu). ĐK \(x \in \mathbb{N}\,;\,\,x \le 25\)

Số câu trả lời sai của bạn Mai là \(25 - x\) (câu)

Số điểm được cộng khi trả lời đúng là \(4x\) (điểm)

Số điểm bị trừ khi trả lời sai là \(1\;{\rm{.}}\;\left( {25 - x} \right)\) (điểm)

Vì bạn Mai đã làm \[25\] câu và đạt hơn \[82\] điểm nên ta có \(4x - \left( {25 - x} \right) \ge 82\)

\(4x - 25 + x \ge 82\)

\(5x \ge 107\)

\(x \ge \frac{{107}}{5}\)

\(x \ge 21,4\)

Mà \(x \in \mathbb{N}\,;\,\,x \le 25\), \(x\) là số nhỏ nhất nên \(x = 22\)

Vậy bạn Mai cần trả lời ít nhất \(22\) câu hỏi đúng để đạt được số điểm trên \(82\) điểm.

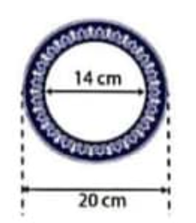
1) Bán kính lớn của viên trắng men xanh của đĩa sứ là \(20:2 = 10\) cm

Bán kính nhỏ của viên trắng men xanh của đĩa sứ là \(14:2 = 7\) cm

Diện tích phần viên trắng men xanh của đĩa sứ là

\(\pi ({R^2} - {r^2}) = \pi ({10^2} - {7^2}) \approx 160(c{m^2})\)

Vậy diện tích phần viên trắng men xanh của đĩa sứ khoảng \(160c{m^2}\)

2)   

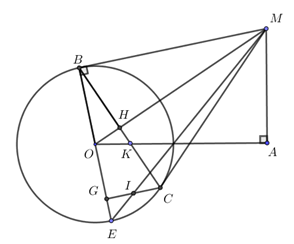
a) \(M,A,B,O\) cùng thuộc 1 đường tròn

\( \Rightarrow \Delta MAO\) vuông tại \(A\) \( \Rightarrow M,A,O\) thuộc đường tròn đường kính \(OM\) \((1)\)

\( \Rightarrow \Delta MBO\) vuông tại \(B\) \( \Rightarrow M,B,O\) thuộc đường tròn đường kính \(OM\) \((2)\)

Từ \((1),(2)\) \( \Rightarrow MABO\) cùng thuộc đường tròn đường kính \(OM\)

b) Xét \(\Delta MBO\) và \(\Delta MCO\) có:

\(MB = MC\) (\(M\) thuộc trung trực của \(BC\))

\(OB = OC( = R)\)

\( \Rightarrow \Delta MBO = \Delta MCO(c.c.c)\)

\( \Rightarrow MCO = MBO = 90^\circ \)

\( \Rightarrow MC \bot OC\) tại \(C \in (O)\)

\( \Rightarrow MC\) là tiếp tuyến của \((O)\)

•  \((g.g)\) \( \Rightarrow \frac{{OK}}{{OM}} = \frac{{OH}}{{OA}}\) \( \Rightarrow OK \cdot OA = OH \cdot OM\)

•  \((g.g)\) \( \Rightarrow \frac{{OH}}{{OB}} = \frac{{OB}}{{OM}}\) \( \Rightarrow OH \cdot OM = O{B^2} = {R^2}\)

\( \Rightarrow OK \cdot OA = OH \cdot OM = {R^2}\)

c) Vì \(GI\,{\rm{//}}\,BM\) \( \Rightarrow \frac{{BM}}{{GI}} = \frac{{BE}}{{GE}} \Rightarrow \frac{{BM}}{{2GI}} = \frac{{2BO}}{{2GE}} \Rightarrow \frac{{BM}}{{2GI}} = \frac{{BO}}{{GE}}(3)\)

 (gg) \( \Rightarrow \frac{{BO}}{{GE}} = \frac{{BM}}{{GC}}\) (4)

Từ (3)(4) \( \Rightarrow \frac{{BM}}{{2GI}} = \frac{{BM}}{{GC}}\)\( \Rightarrow GC = 2GI\)\( \Rightarrow I\) là trung điểm của \(GC\).