$\begin{array}{l}\left( 1 \right) \Leftrightarrow \frac{{x - 3 - 2x + 7}}{{\sqrt {x - 3} + \sqrt {2x - 7} }} = 2\left( {x - 4} \right)\\ \Leftrightarrow \frac{{4 - x}}{{\sqrt {x - 3} + \sqrt {2x - 7} }} = 2\left( {x - 4} \right)\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 4\,\,(TMDK)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{\frac{1}{{\sqrt {x - 3} + \sqrt {2x - 7} }} = - 2}\end{array}} \right. \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 4\,\,(TMDK)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\\{\sqrt {x - 3} + \sqrt {2x - 7} = \frac{{ - 1}}{2}\,\,\,(2)}\end{array}} \right.\end{array}$

Ta có $\left\{ {\begin{array}{*{20}{c}}{\sqrt {x - 3} \ge 0}\\{\sqrt {2x - 7} \ge 0}\end{array}} \right.$ với mọi $x \ge \frac{7}{2}$ nên $\sqrt {x - 3} + \sqrt {2x - 7} \ge 0 > - 2$ với mọi $x \ge \frac{7}{2}.$

Vậy phương trình ban đầu có nghiệm $x = 4.$

2) Cho $a,b$ và $c$ là các số thực khác $0$ thỏa mãn điều kiện ${a^2} - {c^2} = c,{c^2} - {b^2} = b$ và ${b^2} - {a^2} = a.$ Chứng minh $\left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right) = 1.$

Ta có $\left\{ {\begin{array}{*{20}{c}}{{a^2} - {c^2} = c}\\{{c^2} - {b^2} = b}\\{{b^2} - {a^2} = a}\end{array}} \right. \Rightarrow a + b + c = 0$

Ta có ${a^2} - {c^2} = c \Leftrightarrow \left( {a - c} \right)\left( {a + c} \right) = c \Rightarrow \left( {a - c} \right)\left( { - b} \right) = c \Leftrightarrow b\left( {c - a} \right) = c$

Tương tự ta có ${c^2} - {b^2} = b \Rightarrow a\left( {b - c} \right) = b;{b^2} - {a^2} = a \Rightarrow c\left( {a - b} \right) = a.$

Do đó $b\left( {c - a} \right)a\left( {b - c} \right)c\left( {a - b} \right) = abc \Rightarrow \left( {a - b} \right)\left( {b - c} \right)\left( {c - a} \right) = 1$ (do $abc \ne 0).$

Câu 2/5

1) Cho ba số nguyên $a,b$ và $c$ thỏa mãn ${a^2} + {b^2} + {c^2} - 2abc$ chia hết cho $6.$ Chứng minh $abc$ chia hết cho $54.$

2) Tìm tất cả cặp số nguyên dương $\left( {x,y} \right)$ thỏa mãn ${x^3}y - {x^2}y - 4{x^2} + 5xy - {y^2} = 0.$

Xem đáp án

Lời giải

1)· Nếu $a,b,c$ đều không chia hết cho 3 thì \[{a^2},{b^2},{c^2}\] chia cho 3 dư $1.$

$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{a^2} + {b^2} + {c^2}\not \vdots 3}\\{abc\not \vdots 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right. \Rightarrow M\not \vdots 3$ (vô lý)

· Nếu $a,b,c$ có một hoặc hai số không chia hết cho 3 và các số còn lại chia hết cho $3$

$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{{a^2} + {b^2} + {c^2}\not \vdots 3}\\{abc \vdots 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array} \Rightarrow M\not \vdots 3} \right.$ (vô lý)

Vậy $a,b,c \vdots 3 \Rightarrow abc \vdots 27\,\,\left( 1 \right)$

· Lại có, nếu $a,b,c$ đều lẻ thì $\left\{ {\begin{array}{*{20}{c}}{{a^2} + {b^2} + {c^2}\not \vdots 2}\\{2abc \vdots 2\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array} \Rightarrow M\not \vdots 2} \right.$ (vô lý)

Vậy $a,b,c$ có ít nhất một số chẵn $ \Rightarrow abc \vdots 2\,\,\left( 2 \right)$

Từ (1) và (2) $ \Rightarrow abc \vdots 54$ vì $\left( {2,27} \right) = 1.$

2)${x^3}y - {x^2}y - 4{x^2} + 5xy - {y^2} = 0 \Leftrightarrow xy\left( {{x^2} - x + 1} \right) = {\left( {2x - y} \right)^2}\,\,(1)$

Gọi $d = \left( {x;y} \right) \Rightarrow x = da;y = db$ với $\left( {a;b} \right) = 1$ và $a,b,d$ nguyên dương.

Khi đó (1) trở thành ${d^2}ab\left( {{d^2}{a^2} - da + 1} \right) = {d^2}{\left( {2a - b} \right)^2} \Leftrightarrow ab\left( {{d^2}{a^2} - da + 1} \right) = {\left( {2a - b} \right)^2}.$

Suy ra ${\left( {2a - b} \right)^2} \vdots a$ và ${\left( {2a - b} \right)^2} \vdots b$

Ta có ${\left( {2a - b} \right)^2} \vdots a$ mà $\left( {a;b} \right) = 1$$ \Rightarrow \left( {2a - b;a} \right) = 1 \Rightarrow \left( {{{\left( {2a - b} \right)}^2};a} \right) = 1$ do đó $a = 1.$

Từ ${\left( {2a - b} \right)^2} \vdots b$$ \Rightarrow 4{a^2} \vdots b$ mà $\left( {a;b} \right) = 1$$ \Rightarrow 4 \vdots b \Rightarrow \left[ {\begin{array}{*{20}{c}}{b = 1}\\{b = 2}\\{b = 4}\end{array}} \right.\,\,({\rm{do}}\,\,b > 0)$

+) TH1: $a = b = 1 \Rightarrow x = y = d.$

Thay vào giả thiết ta được ${d^4} - {d^3} = 0 \Rightarrow d = 1$ (do $d$ nguyên dương)$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 1}\end{array}.} \right.$

+) TH2: $a = 1;b = 2$ không thỏa mãn.

+) TH3: $a = 1;b = 4$ suy ra $x = d;y = 4d$

Thay vào giả thiết ta được ${d^4} - {d^3} = 0 \Rightarrow d = 1$(do $d$ nguyên dương)$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = 1}\\{y = 4}\end{array}.} \right.$

Thử lại ta thấy cặp số $\left( {x;y} \right) \in \left\{ {\left( {1;1} \right);\left( {1;4} \right)} \right\}$ thỏa mãn yêu cầu bài toán.

Câu 3/5

1) Tìm tất cả cặp số nguyên $\left( {x,y} \right)$ sao cho $xy$ là số chính phương và ${x^2} + xy + {y^2}$ là số nguyên tố.

2) Với các số thực không âm $a,b$ và $c$ thỏa mãn $a + 2b + 3c = 1,$ tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P = \left( {a + 6b + 6c} \right)\left( {a + b + c} \right).$

Xem đáp án

Lời giải

1)Đặt $d = \left( {x;y} \right) \Rightarrow \left\{ {\begin{array}{*{20}{c}}{x = ad}\\{y = bd}\end{array}} \right.$ với $\left( {a;b} \right) = 1$

Suy ra $M = {x^2} + xy + {y^2} = {d^2}\left( {{a^2} + ab + {b^2}} \right)$

Vì ${a^2} + ab + {b^2} \ge 3$ nên $d = 1,$ suy ra $\left( {x;y} \right) = 1.$

Mà $xy$ là số chính phương nên $xy \ge 0;\left| x \right|,\left| y \right|$ đều là số chính phương $ \Rightarrow \left| x \right| = {m^2};\left| y \right| = {n^2}$ với $m,n \in \mathbb{N}.$

$M = {m^4} + {m^2}{n^2} + {n^4} = \left( {{m^2} + mn + {n^2}} \right)\left( {{m^2} - mn + {n^2}} \right)$

Nếu $x = 0$ hoặc $y = 0$ thì $M$ không là số nguyên tố nên $x;y \in {\mathbb{N}^*} \Rightarrow m;n \in {\mathbb{N}^*}$

Do đó ${m^2} + mn + {n^2} \ge 3$

Mà $M$là số nguyên tố nên ${m^2} - mn + {n^2} = 1 \Leftrightarrow {m^2} + {n^2} + {\left( {m - n} \right)^2} = 2 \Rightarrow m = n = 1$

Vậy $\left( {x;y} \right) \in \left\{ {\left( {1;1} \right);\left( { - 1; - 1} \right)} \right\}.$

2) Đặt $x = b + c$

$\left\{ {\begin{array}{*{20}{c}}{2x = 1 - a - c \le 1 - a}\\{3x = 1 + b - a \ge 1 - a}\end{array}} \right.$

- Tìm GTLN của $P$

$P \le \left( {a + 3} \right)\left( {1 - a} \right)\left( {a + \frac{{1 - a}}{2}} \right) = \frac{1}{4}\left( {3 - 2a} \right)\left( {2 + 2a} \right) \le \frac{1}{4}.\frac{{{{\left( {3 - 2a + 2 + 2a} \right)}^2}}}{4} = \frac{{25}}{{16}}$

Vậy GTLN của $P = \frac{{25}}{{16}}.$

Dấu “=” xảy ra khi và chỉ khi $c = 0,a = \frac{1}{4},b = \frac{3}{8}.$

- Tìm GTNN của $P$

$P \ge \left[ {a + 2\left( { - a} \right)} \right]\left[ {a + \frac{{1 - a}}{3}} \right] = \frac{1}{3}\left( {2{a^2} + 5a + 2} \right) \ge \frac{2}{3}.$

Dấu “=” xảy ra khi và chỉ khi $a = b = 0,c = \frac{1}{3}.$

Câu 4/5

Cho tam giác $ABC$ có ba góc nhọn \[\left( {AB < AC} \right),\] nội tiếp đường tròn $\left( O \right).$Ba đường cao $AD,BE$ và $CF$ của tam giác $ABC$ cùng đi qua điểm $H.$ Đường thẳng $EF$ cắt đường thẳng $AD$ tại điểm $Q.$ Gọi $M$ và $I$ lần lượt là trung điểm của các đoạn thẳng $BC$và $AH.$ Đường thẳng $IM$ cắt đường thẳng $EF$ tại điểm $K.$

1)    Chứng minh tam giác $AEK$ đồng dạng với tam giác $ABM.$

2)    Đường thẳng $EF$ cắt đường thẳng $BC$ tại điểm $S,$ đường thẳng $SI$cắt đường thẳng $MQ$ tại điểm $T.$ Chứng minh bốn điểm $A,T,H$ và $M$ cùng thuộc một đường tròn.

3)    Tia $TH$ cắt đường tròn $\left( O \right)$ tại điểm $P.$ Chứng minh ba điểm $A,K$ và $P$ là ba điểm thẳng hàng.

Xem đáp án

Lời giải

$Cho tam giác $ABC$ có ba góc nhọn ( {AB < AC),\] nội tiếp đường tròn (ảnh 1)$

1) $I$ là tâm đường tròn ngoại tiếp $AFHE$ (nội tiếp)

$M$ là tâm đường tròn ngoại tiếp $BFEC$ (nội tiếp)

$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{IM \bot EF}\\{EK = KF}\end{array}} \right.$ (đường nối tâm)

$ \Rightarrow \left\{ {\begin{array}{*{20}{c}}{\frac{{AE}}{{AB}} = \frac{{EF}}{{BC}} = \frac{{2KE}}{{2BM}} = \frac{{KE}}{{BM}}}\\{\widehat {AEF} = \widehat {ABC}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,}\end{array}} \right.$

$Cho tam giác $ABC$ có ba góc nhọn ( {AB < AC),\] nội tiếp đường tròn (ảnh 2)$

2)Có $\widehat {AEH} = \widehat {AFH} = {90^0}$ suy ra tứ giác $AEHF$ nội tiếp đường tròn tâm $I$ đường kính $AH.$

Có $\widehat {BEC} = \widehat {BFC} = {90^0}$ suy ra tứ giác $BFEC$ nội tiếp đường tròn tâm $M$ đường kính $BC.$

Suy ra $IM \bot EF$ tại $K$ hay $SK \bot IM.$

Suy ra $Q$ là trực tâm của $\Delta ISM \Rightarrow MT \bot ST$ tại $T.$

Ta có $\widehat {MTI} = \widehat {MDI} = {90^0} \Rightarrow $ Tứ giác \[ITDM\] nội tiếp đường tròn đường kính $IM\,\,(1)$

Ta có $IA = IE \Rightarrow \Delta IEA$ cân tại $I \Rightarrow \widehat {MEC} = \widehat {MCE}.$

Mà $\widehat {IAE} + \widehat {MCE} = {90^0}$ suy ra $\widehat {IEA} + \widehat {MEC} = {90^0}$ suy ra $\widehat {MEI} = {90^0}.$

Tương tự ta cũng có $\widehat {MFI} = {90^0}$ do đó $E,F$ cùng thuộc đường tròn đường kính $IM.$ (2)

Từ (1) và (2) suy ra các điểm $I,T,F,M,E$cùng thuộc đường tròn đường kính $IM.$

Suy ra $QT.QM = QE.QF.$

Lại có tứ giác $AFHE$ nội tiếp suy ra $QF.QE = QH.QA.$

Từ đó suy ra $QT.QM = QH.QA$ suy ra tứ giác $ATHM$ nội tiếp.

$Cho tam giác $ABC$ có ba góc nhọn ( {AB < AC),\] nội tiếp đường tròn (ảnh 3)$

3)Ta có $AO \bot EF$

$ \Rightarrow \widehat {KAO} = \widehat {DAM} \Rightarrow \widehat {DAK} = \widehat {MAO} = \widehat {AMI}\left( {IM\parallel AO} \right)$

Có $\widehat {AMI} = \widehat {AMT} - \widehat {TMI} = \widehat {AHT} - \widehat {IDT} = \widehat {DTH}$ (do \[ATHM\]nội tiếp; $TIMD$ nội tiếp)

Trên tia đối $HT$ lấy điểm $P'$ sao cho $ATDP'$ nội tiếp $ \Rightarrow \widehat {DAP'} = \widehat {DTH} = \widehat {AMI} = \widehat {DAK}$

$ \Rightarrow A,K,P'$ thẳng hàng (1)

Do $ATDP'$ nội tiếp $ \Rightarrow HT.HP' = HD.HA = HB.HE = HC.HF$

$ \Rightarrow BP'ET$ nội tiếp $ \Rightarrow \widehat {TP'B} = \widehat {TEH}$

Tương tự: $\widehat {TP'C} = \widehat {TFH}$

Ta có: $\widehat {FTE} = \widehat {FIE} = 2\widehat {BAC}$ (do $FTIE$ nội tiếp)

$ \Rightarrow \widehat {TEH} + \widehat {TFH} = {360^0} - \widehat {FTE} - \widehat {FHE} = {360^0} - 2.\widehat {BAC} - \left( {{{180}^0} - \widehat {BAC}} \right) = {180^0} - \widehat {BAC}$

$\begin{array}{l} \Rightarrow \widehat {BP'C} = \widehat {TP'C} + \widehat {TP'B} = {180^0} - \widehat {BAC}\\ \Rightarrow \widehat {BP'C} + \widehat {BAC} = {180^0}\end{array}$

$ \Rightarrow ABP'C$ nội tiếp $ \Rightarrow P' \in \left( O \right) \Rightarrow P' \equiv P$ (2).

Từ (1) và (2) ta suy ra $A,K,P$ thẳng hàng.

Câu 5/5

Cho $2023$ điểm nằm trong một hình vuông cạnh $1.$ Một tam giác đều được gọi là phủ điểm $M$nếu điểm $M$nằm trong tam giác hoặc nằm trên cạnh của tam giác.

1) Chứng minh tồn tại tam giác đều cạnh $\frac{1}{{\sqrt 2 }}$ phủ ít nhất $253$ điểm trong $2023$ điểm đã cho.

2) Chứng minh tồn tại tam giác đều cạnh $\frac{{11}}{{12}}$ phủ ít nhất $506$ điểm trong $2023$ điểm đã cho.

Xem đáp án

Lời giải

a) Dựng 8 tam giác đều có cạnh bằng $\frac{1}{{\sqrt 2 }}$ phủ hoàn toàn hình vuông như hình vẽ dưới do

$2023 = 252.8 + 7$ nên có ít nhất một tam giác đều phủ ít nhất 253 điểm.

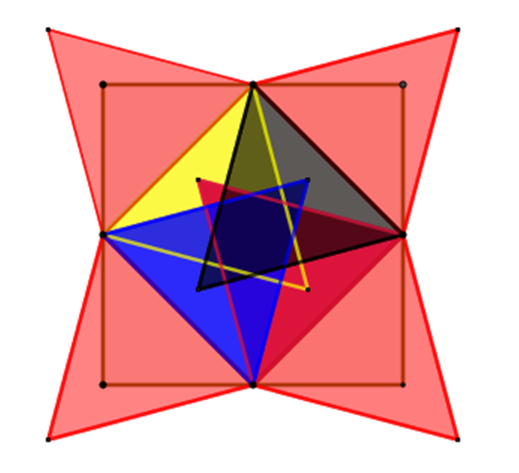
$Cho $2023$ điểm nằm trong một hình vuông cạnh $1.$ Một tam giác đều được gọi là (ảnh 1)$

b) Dựng $MNP$ tam giác đều có cạnh bằng $\frac{{11}}{{12}}$ đi qua tâm $O$của hình vuông như hình vẽ dưới

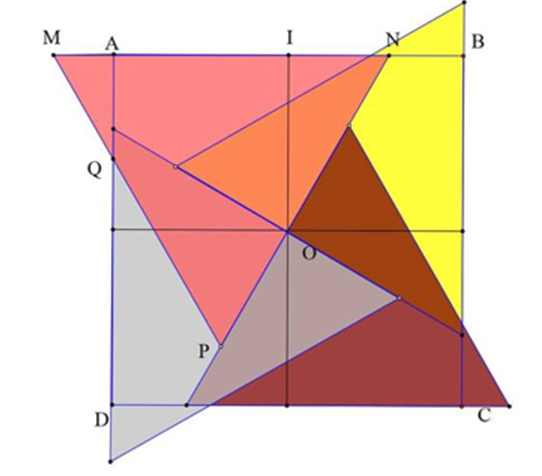
$Cho $2023$ điểm nằm trong một hình vuông cạnh $1.$ Một tam giác đều được gọi là (ảnh 2)$

Ta có: $IN = \frac{1}{{2\sqrt 3 }} \Rightarrow NB = \frac{1}{2} - \frac{1}{{2\sqrt 3 }}$ và $AQ = MA.\sqrt 3 = \left( {\frac{{11}}{{12}} - \frac{1}{2} - \frac{1}{{2\sqrt 3 }}} \right)\sqrt 3 $ ta thấy $AQ > NB$ nên bốn tam giác đều có cạnh bằng $\frac{{11}}{{12}}$ phủ kín hình vuông có cạnh bằng 1. Mặt khác ta có $2023 = 4.505 + 3$ nên có ít nhất một tam giác đều phủ ít nhất $506$ điểm.

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tiếng Anh

Công nghệ

Tin học

ĐHQG Hà Nội

ĐHQG Hồ Chí Minh

ĐH Bách Khoa Hà Nội

ĐHSP Hà Nội

Bộ Công an

Bộ Quốc phòng

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Tin học

Global success

iLearn Smart World

Friends Global

Bright

Explore new worlds

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý

Hóa học

Sinh học

Văn

Lịch sử

Địa lý

Giáo dục Kinh tế và Pháp luật

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Toán

Vật lý