b) \[\left\{ \begin{array}{l}x + y = 8\\2x - y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x = 9\\y = 8 - x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 3\\y = 5\end{array} \right..\]

Câu 2

Trong mặt phẳng tọa độ Oxy, cho đường thẳng \[\left( d \right):y = 6x + 2023\] và parabol \[\left( P \right):y = {x^2}.\]

a)       Vẽ parabol \[\left( P \right).\]

b)       Chứng minh \[\left( d \right)\] cắt \[\left( P \right)\] tại hai điểm phân biệt.

c)       Gọi \[{x_1}\] và \[{x_2}\] là hoành độ giao điểm của \[\left( d \right)\] và \[\left( P \right).\] Tính \[{x_1} + {x_2}\] và \[{x_1} \cdot {x_2}.\] Từ đó lập phương trình bậc hai ẩn t có hai nghiệm \[{t_1} = {x_1} + 2{x_2}\] và \[{t_2} = {x_2} + 2{x_1}.\]

Xem đáp án

Lời giải

a) Bảng giá trị

x	\[ - 2\]	\[ - 1\]	0	1	2
\[y = {x^2}.\]	4	1	0	1	4

Đồ thị

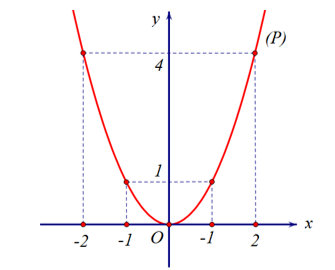
Trong mặt phẳng tọa độ Oxy, cho đường thẳng (ảnh 1)

b) Phương trình hoành độ giao điểm của \[\left( d \right)\] và \[\left( P \right):\]

\[{x^2} = 6x + 2023 \Leftrightarrow {x^2} - 6x - 2023 = 0\,\,\,\,\,\,\,\,\left( * \right)\]

Vì \[\Delta = {\left( { - 6} \right)^2} - 4 \cdot 1 \cdot \left( { - 2023} \right) = 8128 > 0\] nên phương trình (*) có hai nghiệm phân biệt.

Vậy \[\left( d \right)\] cắt \[\left( P \right)\] tại hai điểm phân biệt.

Cách 2:

Ta có: \(a.c = 1.( - 2023) = - 2023 < 0\)

Nên phương trình luôn có hai nghiệm phân biệt trái dấu

Vậy \(\left( d \right)\) luôn cắt \(\left( P \right)\) tại hai điểm phân biệt.

c) Theo Vi-et ta có \[\left\{ \begin{array}{l}{x_1} + {x_2} = - \frac{{ - 6}}{1} = 6\\{x_1} \cdot {x_2} = - 2023.\end{array} \right.\]

Suy ra: \[\left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = (}}{x_1}{\rm{ + 2}}{x_2}{\rm{) + (}}{x_2}{\rm{ + 2}}{x_1})\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = {\rm{(}}{x_1}{\rm{ + 2}}{x_2}{\rm{)}}{\rm{.(}}{x_2}{\rm{ + 2}}{x_1})\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = }}{x_1}{\rm{ + 2}}{x_2}{\rm{ + }}{x_2}{\rm{ + 2}}{x_1}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = {x_1}{x_2}{\rm{ + 2}}x_1^2{\rm{ + 2}}x_2^2 + 4{x_1}{x_2}\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 3}}{x_1}{\rm{ + 3}}{x_2}{\rm{ }}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = 5{x_1}{x_2}{\rm{ + 2}}\left( {x_1^2{\rm{ + }}x_2^2} \right)\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 3}}{\rm{.(}}{x_1}{\rm{ + }}{x_2}{\rm{) }}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = 5{x_1}{x_2}{\rm{ + 2}}\left[ {{{\left( {{x_1}{\rm{ + }}{x_2}} \right)}^2} - 2{x_1}{x_2}} \right]\end{array} \right.\]

\[ \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 3}}{\rm{.6 }}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = 5.( - 2023){\rm{ + 2}}\left[ {{6^2} - 2.( - 2023)} \right]\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 18 }}\\{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = - 1951\end{array} \right.\]

Đặt \[{\rm{S = }}{{\rm{t}}_1}{\rm{ + }}{{\rm{t}}_2}{\rm{ = 18}}\] ; \[{\rm{P = }}{{\rm{t}}_1}{\rm{.}}{{\rm{t}}_2} = - 1951\]

Do \[{{\rm{S}}^2} - 4.P = {18^2} - 4.( - 1951) = 8128 > 0\]

nên theo định lí Vi-et đảo ta có \[{{\rm{t}}_1}{\rm{ ; }}{{\rm{t}}_2}\] là hai nghiệm của phương trình bậc hai

\({t^2} - S.t + P = 0\)

\( \Leftrightarrow {t^2} - 18t - 1951 = 0\)

Vậy phương trình bậc hai ẩn t cần tìm là: \({t^2} - 18t - 1951 = 0\)

Câu 3

a) Hưởng ứng phong trào “ Ngày chủ nhật xanh” do Tỉnh đoàn phát động. Trường THCS X chọn 15 học sinh chia thành hai tổ tham gia trồng cây. Tổ 1 trồng được 30 cây, tổ II trồng được 36

cây. Biết rằng mỗi học sinh ở tổ I trồng được nhiều hơn mỗi học sinh ở tổ II là 1 cây. Hỏi mỗi tổ có bao nhiêu học sinh?

b) Gạch xây 3 lỗ (Như hình vẽ) được làm bằng đất nung, thường được sử dụng trong các công trình có dạng hình hộp chữ nhật với chiều dài 220 mm, chiều rộng 105 mm, chiều cao 60 mm. Mỗi lỗ là hình trụ có trục song song với chiều cao viên gạch, đường kính đáy là 14 mm. Tính thể tích phần đất nung của một viên gạch. Biết V = abc; \(V = \pi {r^2}.h\) lần lượt là công thức tính thể tích hình hộp chữ nhật và hình trụ (trong đó a, b, c là ba kích thước của hình hộp chữ nhật, r là bán kính đường tròn đáy, h là chiều cao hình trụ, lấy \(\pi \approx 3,14\))

Xem đáp án

Lời giải

Cách 1: Lập hệ phương trình

Gọi x; y (Học sinh) lần lượt là số học sinh của tổ I và tổ II. (\[x,y \in {N^*}\]và x, y < 15)

Theo đề ta có: \(x + y = 15\) (1)

Số cây mỗi học sinh tổ I trồng được là: \(\frac{{30}}{x}\) (cây)

Số cây mỗi học sinh tổ II trồng được là: \(\frac{{36}}{y}\) (cây)

Mỗi học sinh ở tổ I trồng được nhiều hơn mỗi học sinh ở tổ II là 1 cây nên ta có\(\frac{{30}}{x} - \frac{{36}}{y} = 1\) (2)

Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}x + y = 15\\\frac{{30}}{x} - \frac{{36}}{y} = 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 15 - y\\\frac{{30}}{{15 - y}} - \frac{{36}}{y} = 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 15 - y\\\frac{{30y - 36\left( {15 - y} \right)}}{{y\left( {15 - y} \right)}} = \frac{{y\left( {15 - y} \right)}}{{y\left( {15 - y} \right)}}\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}x = 15 - y\\30y - 540 + 36y = 15y - {y^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 15 - y\\{y^2} + 51y - 540 = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x = 15 - y\\(y - 9)(y + 60) = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 15 - y\\\left[ \begin{array}{l}y = 9(tm)\\y = - 60(ktm)\end{array} \right.\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 15 - 9 = 6\\y = 9\end{array} \right.\)

Vậy: Số học sinh của tổ I là 6 (Học sinh)

Số học sinh của tổ II là 9 (Học sinh)

Cách 2: Lập phương trình bậc hai

	Số học sinh	Số cây / 1hs	Số cây trồng được
Tổ I	x	\[\frac{{30}}{x}\]	30
Tổ II	15 - x	\[\frac{{36}}{{15 - x}}\]	36
	ð Phương trình: \[\frac{{30}}{x} - \frac{{36}}{{15 - x}} = 1\]

Gọi số học sinh của Tổ I là \(x\) (học sinh) \(\left( {x \in {N^*};x < 15} \right)\)

Khi đó, số học sinh của Tổ II là \(15 - x\) (học sinh)

Mỗi học sinh tổ I trồng được \[\frac{{30}}{x}\] (cây)

Mỗi học sinh tổ I trồng được \[\frac{{36}}{{15 - x}}\] (cây)

Theo đề bài, ta có phương trình :

\[\frac{{30}}{x} - \frac{{36}}{{15 - x}} = 1\]

\[ \Leftrightarrow 30.(15 - x) - 36x = 1.x.(15 - x)\]

\[ \Leftrightarrow 450 - 30x - 36x = 15x - {x^2}\]

\[ \Leftrightarrow {x^2} - 15x + 450 - 30x - 36x = 0\]

\[ \Leftrightarrow {x^2} - 81x + 450 = 0\]

\(... \Rightarrow \left[ \begin{array}{l}{x_1} = 75(L) & \\{x_2} = 6 & (t/m)\end{array} \right.\)

Vậy tổ I có 6 học sinh ; tổ II có 9 học sinh.

b)Thể tích viên gạch hình hộp chữ nhật khi chưa khoét lỗ là:

\({V_1} = a.b.c = 220.105.60 = 1386000\) (mm3)

Thể tích mỗi lỗ hình trụ trong viên gạch là:

\({V_2} = \pi {r^2}h = \pi .{\left( {\frac{{40}}{2}} \right)^2}.60 = 9231,6\) (mm3)

Thể tích phần đất nung của viên gạch là:

\(V = {V_1} - 3.{V_2} = 1386000 - 3.9231,6 = 1358305,2\)(mm3)

Vây: Thể tích phần đất nung của viên gạch là 1358305,2 mm3.

Câu 4

Cho đường tròn (O) đường kính AB và điểm C thuộc đường tròn sao cho AC < BC (C khác A). Vẽ CH vuông góc với AB (H \[ \in \] AB).

a) Chứng minh \[\Delta ABC\] là tam giác vuông. Tính AC, biết AB = 4cm, AH = 1cm.

b) Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Vẽ DE vuông góc với AB (E\[ \in \]AB). Chứng minh BECD là tứ giác nội tiếp.

c) Gọi I là giao điểm của DE và BC, K là điểm đối xứng của I qua C, tiếp tuyến của (O) tại C cắt KA tại M. Chứng minh KA là tiếp tuyến của (O) và BM đi qua trung điểm của CH.

Xem đáp án

Lời giải

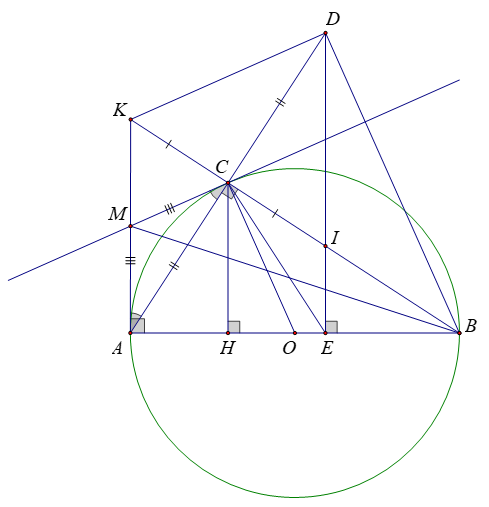
Cho đường tròn (O) đường kính AB và điểm C thuộc đường tròn sao cho AC < BC (C khác A). Vẽ CH (ảnh 1)

a) Chứng minh \[\Delta ABC\] là tam giác vuông. Tính AC, biết AB = 4cm, AH = 1cm.

+ Xét đường tròn (O) có \[\widehat {ACB}\] là góc nội tiếp chắn nửa đường tròn

\[ \Rightarrow \]\[\widehat {ACB}\] = 900 hay \[\Delta ABC\] vuông tại C

+ \[\Delta ABC\] vuông tại C có CH là đường cao

\[ \Rightarrow \]\[A{C^2} = AH.AB = 1.4 = 4\] (Hệ thức lượng trong tam giác vuông)

\[ \Rightarrow AC = 2cm\]

b) Trên tia đối của tia CA lấy điểm D sao cho CD = CA. Vẽ DE vuông góc với AB (E\[ \in \]AB). Chứng minh BECD là tứ giác nội tiếp.

+ Xét tứ giác BECD có \[\widehat {DCB} = \widehat {DEB}\]

Mà chúng ở vị kề nhau cùng nhìn cạnh DB

Nên tứ giác BECD nội tiếp

c) Gọi I là giao điểm của DE và BC, K là điểm đối xứng của I qua C, tiếp tuyến của (O) tại C cắt KA tại M. Chứng minh KA là tiếp tuyến của (O) và BM đi qua trung điểm của CH.

+ Tứ giác AKDI có CK = CI (K là điểm đối xứng của I qua C) và CA = CD

\[ \Rightarrow \] Tứ giác AKDI là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường)

\[ \Rightarrow \] AK \[\parallel \] DI mà DI \[ \bot \] AO tại E

\[ \Rightarrow \] AK \[ \bot \] AO tại A

Mà AO là bán kính của đường tròn (O) nên AK là tiếp tuyến của đường tròn (O) tại A.

+ Đường tròn (O) có MA, MC là 2 tiếp tuyến cắt nhau \[ \Rightarrow \] MA = MC (1)

\[ \Rightarrow \]\[\Delta MAC\] cân tại M \[ \Rightarrow \] \[\widehat {MAC} = \widehat {MCA}\]

Mà \[\widehat {KCM} + \widehat {MCA} = {90^0}\] nên \[\widehat {KCM} + \widehat {MAC} = {90^0}\]

Mà \[\widehat {MKC} + \widehat {MAC} = {90^0}\] (\[\Delta AKC\] vuông tại C) nên \[\widehat {KCM} = \widehat {MKC}\]

\[ \Rightarrow \]\[\Delta KMC\] cân tại M \[ \Rightarrow \]MC = MK (2)

+ Từ (1) và (2) \[ \Rightarrow \] MA = MK hay BM đi qua trung điểm của CH

+ Gọi U là giao điểm của CH và MB

+ AK // CH (cùng \[ \bot \] AB)

+ MK // CU\[ \Rightarrow \frac{{CU}}{{MK}} = \frac{{BU}}{{BM}}\](Hệ quả định lý Talet) (3)

+ MA // UH \[ \Rightarrow \frac{{HU}}{{AM}} = \frac{{BU}}{{BM}}\](Hệ quả định lý Talet) (4)

+ Từ (3), (4) và MK = AM \[ \Rightarrow CU = HU\] hay U là trung điểm của CH

Vậy BM đi qua trung điểm của CH

Câu 5

Trong quá trình thiết kế công viên thiếu nhi, kĩ sư sử dụng mảnh đất hình chữ nhật có diện tích 600 m2 để làm bãi đỗ xe. Một cạnh của mảnh đất được xây bằng tường gạch với mỗi mét chiều dài chi phí hết 280 000 đồng, ba cạnh còn lại được rào bằng một loại thép với mỗi mét chiều dài chi phí hết 140 000 đồng, trong đó có mở cổng rộng 5 m (như hình vẽ). Tìm chu vi của mảnh đất sao cho chi phí làm hàng rào là ít nhất.

Xem đáp án

Lời giải

Gọi x và y (m) lần lượt là độ dài cạnh được xây bằng tường và cạnh được rào bằng thép \[\left( {x,\,\,y > 0} \right)\]

Diện tích của mảnh đất là \[x \cdot y = 600\] (m2)

Chi phí xây tường gạch là \[280\,x\] (nghìn đồng)

Chi phí rào bằng thép là \[140\,\left( {2y + x - 5} \right)\] (nghìn đồng)

Tổng chi phí làm hàng rào là \[C = 420x + 280y - 700\] (nghìn đồng)

Chu vi mảnh đất bằng \[2\left( {x + y} \right)\] (m)

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Tiếng Anh

Giáo dục Kinh tế và Pháp luật

ĐHQG Hồ Chí Minh

ĐH Bách Khoa

ĐHQG Hà Nội

Bộ Công an

ĐHSP Hà Nội

Bằng lái xe

English Test

IT Test

Đại học

Viên chức

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Tin học

Giáo dục Kinh tế và Pháp luật

Global success

iLearn Smart World

Friends Global

Explore new worlds

Bright

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý

Hóa học

Lịch sử

Địa lý

Sinh học

Công nghệ

Tin học

Giáo dục Quốc Phòng và An Ninh

Giáo dục Kinh tế và Pháp luật

Toán

Văn

Vật lý