Đề thi tuyển sinh vào lớp 10 Toán năm học 2015 - 2016 Sở GD&ĐT TP.HCM có đáp án

\[{x^2} - 8x + 15 = 0\]

Ta có: \[\Delta  = {4^2} - 15 = 1\]

Vậy phương trình có hai nghiệm phân biệt \({x_1} = 5,\,{x_2} = 3\).

2{x^2} - \sqrt 2 x - 2 = 0\]

Ta có: \[\Delta  = 2 - 4.2.\left( { - 2} \right) = 18\]

Khi đó phương trình đã cho có hai nghiệm phân biệt

\[{x_1} = \frac{{\sqrt 2  + 3\sqrt 2 }}{4} = \sqrt 2 ;\,\,{x_2}\,{\rm{ = }}\frac{{\sqrt 2  - 3\sqrt 2 }}{4} = \frac{{ - \sqrt 2 }}{2}\].

\({x^4} - 5{x^2} - 6 = 0\)

Đặt \(u = {x^2}\,\,\left( {u \ge 0} \right)\), phương trình đã cho trở thành:

\[\begin{array}{l}{u^2} - 5u - 6 = 0\\ \Leftrightarrow \left[ \begin{array}{l}u =  - 1\,\,\,\,(l)\\u = 6\,\,\,\,\left( {tm} \right)\end{array} \right.\end{array}\]

Với \[u - 6 \Rightarrow {x^2} = 6 \Leftrightarrow x =  \pm \sqrt 6 \].

Vậy phương trình đã cho có hai nghiệm phân biệt \(x =  \pm \sqrt 6 \).

\[\left\{ \begin{array}{l}2x + 5y =  - 3\\3x - y = 4\end{array} \right.\]\[ \Leftrightarrow \left\{ \begin{array}{l}17x = 17\\3x - y = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y =  - 1\end{array} \right.\].

Hệ phương trình có nghiệm duy nhất \(\left( { - 1;\,\,1} \right)\).

a) Đồ thị:

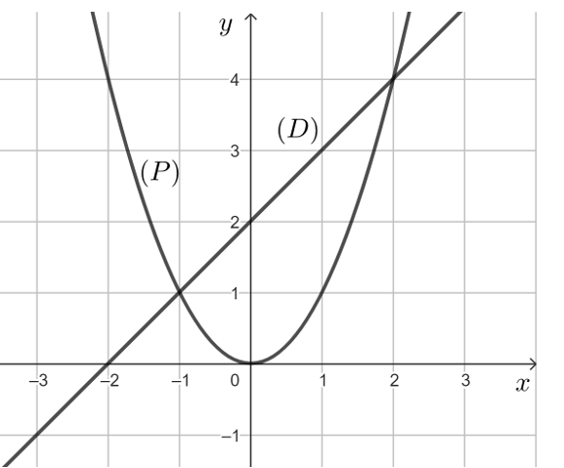
Lưu ý: \(\left( P \right)\) đi qua các điểm (0; 0), (1; 1), (2; 4), (– 1; 1), (– 2; 4).

\(\left( D \right)\) đi qua (-1; 1), (2; 4)

b) Phương trình hoành độ giao điểm của \(\left( P \right)\) và \(\left( D \right)\) là

\[\begin{array}{l}{x^2} = x + 2 \Leftrightarrow {x^2} - x - 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 2\end{array} \right.\end{array}\]

Với \(x =  - 1\) thì \(y = 1\), với \(x = 2\) thì \(y = 4\).

Vậy toạ độ các giao điểm của \(\left( P \right)\) và \(\left( D \right)\) là (-1; 1), (2; 4).

+) \[A = \frac{{\sqrt x }}{{\sqrt x  - 2}} + \frac{{\sqrt x  - 1}}{{\sqrt x  + 2}} + \frac{{\sqrt x  - 10}}{{x - 4}}\,\,\left( {x \ge 0,x \ne 4} \right)\]

Với điều kiện \(x \ge 0,\,\,x \ne 4\), ta có:

\[A = \frac{{\sqrt x }}{{\sqrt x  - 2}} + \frac{{\sqrt x  - 1}}{{\sqrt x  + 2}} + \frac{{\sqrt x  - 10}}{{x - 4}}\,\,\]

\[ = \frac{{\sqrt x \left( {\sqrt x  + 2} \right) + \left( {\sqrt x  - 1} \right)\left( {\sqrt x  - 2} \right) + \sqrt x  - 10}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\]

\[ = \frac{{x + 2\sqrt x  + \left( {x - 3\sqrt x  + 2} \right) + \sqrt x  - 10}}{{x - 4}} = \frac{{2x - 8}}{{x - 4}} = 2\].

+) \[B = \left( {13 - 4\sqrt 3 } \right)\left( {7 + 4\sqrt 3 } \right) - 8\sqrt {20 + 2\sqrt {43 + 24\sqrt 3 } } \]

\[ = {\left( {2\sqrt 3  - 1} \right)^2}.{\left( {2 + \sqrt 3 } \right)^2} - 8\sqrt {20 + 2\sqrt {{{\left( {4 + 3\sqrt 3 } \right)}^2}} } \]

\[ = {\left( {3\sqrt 3  + 4} \right)^2} - 8\sqrt {20 + 2\left( {4 + 3\sqrt 3 } \right)} \]

\[ = {\left( {3\sqrt 3  + 4} \right)^2} - 8\sqrt {{{\left( {3\sqrt 3  + 1} \right)}^2}} \]

\[ = 43 + 24\sqrt 3  - 8\left( {3\sqrt 3  + 1} \right)\]

\[ = 43 + 24\sqrt 3  - 24\sqrt 3  - 8\]

\[ = 35\]