7881 câu Trắc nghiệm tổng hợp môn Toán 2023 cực hay có đáp án (Phần 38)
63 người thi tuần này 4.6 60 K lượt thi 92 câu hỏi 100 phút
🔥 Đề thi HOT:
5920 câu Trắc nghiệm tổng hợp môn Toán 2023 có đáp án (Phần 1)
135 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu cực hay có lời giải (P1)
80 câu Trắc nghiệm Tích phân có đáp án (Phần 1)
15 câu Trắc nghiệm Số phức có đáp án (Vận dụng)
80 câu Bài tập Hình học Khối đa diện có lời giải chi tiết (P1)
7 câu Trắc nghiệm Khối đa diện lồi và khối đa diện đều có đáp án (Vận dụng)
148 câu Bài tập Hình học mặt nón, mặt trụ, mặt cầu từ đề thi Đại học có lời giải (P1)
62 câu Trắc nghiệm Khái niệm về khối đa diện (nhận biết)
Nội dung liên quan:
Danh sách câu hỏi:
Câu 9:
Cho dãy số (un) là một cấp số cộng, biết u2 + u21 = 50. Tính tổng của 22 số hạng đầu của dãy.
Câu 28:
Tìm tất cả các giá trị của b để hàm số y = x2 + 2(b + 6)x + 4 đồng biến trên khoảng (6; +∞).
Câu 29:
Tìm tất cả các giá trị của tham số m để hàm số y = x3 − 2mx2 + m2x + 2 đạt cực tiểu tại x = 1.
Câu 38:
Cho hàm số y = f (x) có đồ thị đạo hàm y = f ′(x) như hình bên.
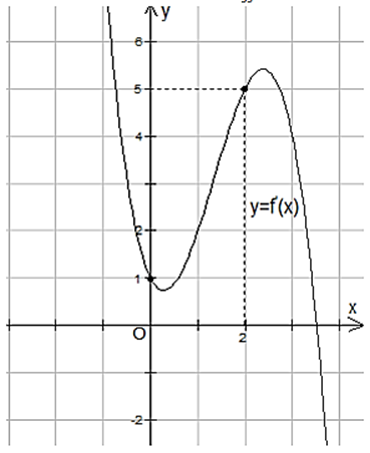
Khẳng định nào sau đây là đúng?
Cho hàm số y = f (x) có đồ thị đạo hàm y = f ′(x) như hình bên.

Khẳng định nào sau đây là đúng?
Câu 77:
Trong mặt phẳng Oxy cho A(−2m; − m), B(2m; m). Với giá trị nào của m thì đường thẳng AB đi qua O?
11994 Đánh giá
50%
40%
0%
0%
0%